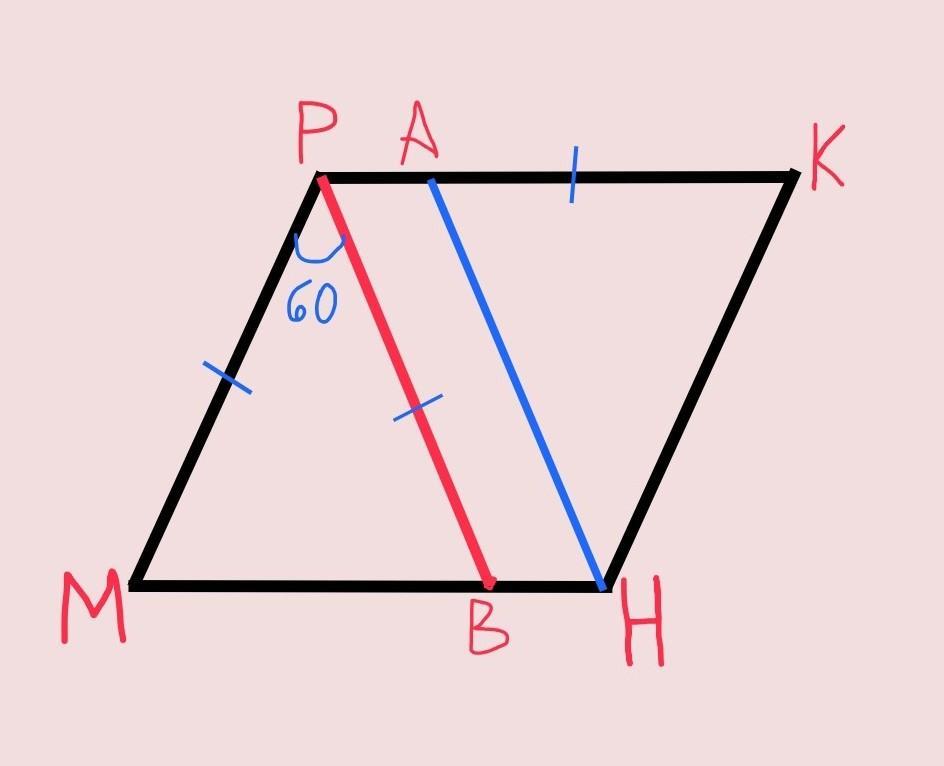
на сторонах PK и MH параллелограмма MPKH взяты точки A и B соответственно , MP=PB=AK , угол MPB =60°. найдите углы параллелограмма и сравните отрезки BM и AH. помогите побыстрее
Ответы
Объяснение:
Так как МР=РВ по условию, то ∆МРВ – равнобедренный. Углы при основании равнобедренного треугольника равны, а сумма всех углов равна 180°.
Тогда угол PMB=угол РВМ=(180°–МРВ)÷2=(180°–60°)÷2=60°.
Получим что все углы ∆МРВ равны 60°, тогда ∆МРВ – равносторонний.
Тогда МВ=МР.
Углы при одной стороне параллелограмма в сумме равны 180°.
Значит угол МРК=180°–угол РМВ=180°–60°=120°
Противоположные углы параллелограмма равны.
Следовательно угол РКН=угол РМН=60°; угол МНК=угол МРК=120°.
МР=АК по условию
МР=КН так как противоположные стороны параллелограмма равны.
Углы при основании равнобедренного треугольника равны, а сумма всех углов равна 180°.
Следовательно: угол КАН=угол КНА=(180°–угол АКН)÷2=(180°–60°)÷2=60°.
Получим что все углы ∆АКН равны 60°, тогда ∆АКН – равносторонний. Исходя из этого АН=АК
МВ=МР=АК=АН => МВ=АН.
Ответ: 1) 60°; 120; 2) равны.