Question

Помогите!!!

Радиус окружности, описанной около равнобедренного треугольника с углом 120°, равен 6√3см.

Найдите стороны треугольника (25 баллов).

Answer 1

Ответ:

$6\sqrt{3}$ см ; $6\sqrt{3}$ см и 18 см.

Объяснение:

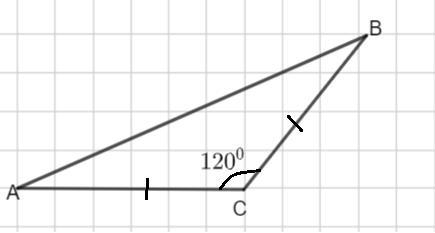
Рассмотрим Δ АВС - равнобедренный.

АС=ВС.

∠С=120°.

Так как в равнобедренном треугольнике углы при основании равны и сумма всех углов треугольника равна 180 °, то

∠А=∠В= (180°-120°) : 2=60°: 2= 30°.

Радиус окружности, описанной около треугольника находится по формуле

$R= \dfrac{a}{2sin\alpha } ,$

где α - угол, лежащий напротив стороны а.

Тогда

$R= \dfrac{AB}{2sin120^{0} } \\\\AB=2Rsin120^{0}$

По условию

$R=6\sqrt{3}$ см.

Значит,

$AB=2\cdot 6\sqrt{3} \cdot \dfrac{\sqrt{3} }{2} =6\cdot 3=18$    см.

$R= \dfrac{AC}{2sin30^{0} } \\\\AC=2Rsin30^{0};\\AC=2\cdot 6\sqrt{3} \cdot \dfrac{1}{2} =6\sqrt{3}$

AC=BC= $6\sqrt{3}$   см