Предмет: Алгебра,
автор: suleymenovbiken5
ДАЮ 25 БАЛЛОВ ТОМУ КТО ОТВЕТИТ. Изобразите множество точек, заданных системой неравенств: x2+y2<49;хy≤5.
Ответы
Автор ответа:
21
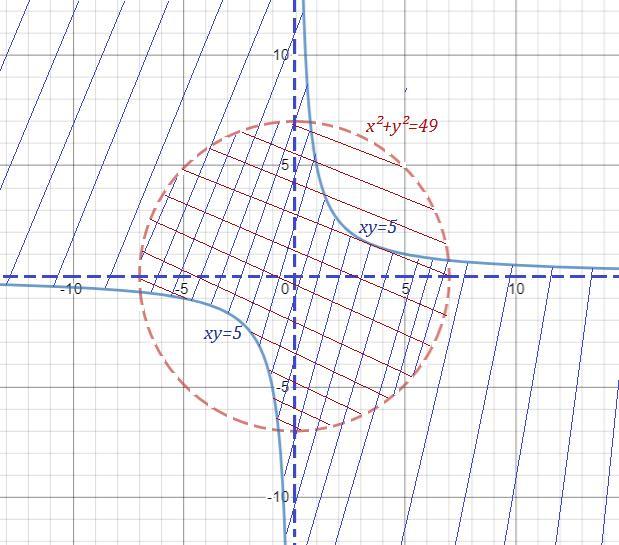
x²+y²<49 - это область внутри окружности с центром (0,0) и R=7, граница не входит в область . Красная штриховка .
xy=5 - это гипербола. Область xy≤5 при х≥0 (в правой полуплоскости) лежит ниже линии гиперболы. Область ху≤5 при х <0 (в левой полуплоскости) лежит выше линии гиперболы. Граница входит в область . Синяя штриховка .
На рисунке искомая область заштрихована пересечением синих и красных линий.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: yaignatovitch
Предмет: География,
автор: ferdji83
Предмет: Русский язык,
автор: Liliya2006
Предмет: Алгебра,
автор: 4e4iik
Предмет: Математика,
автор: lizacat1502