Предмет: Математика,
автор: aegot110513
решите иррациональное неравенство. максимально подробно пожалуйста. не через одз
Приложения:
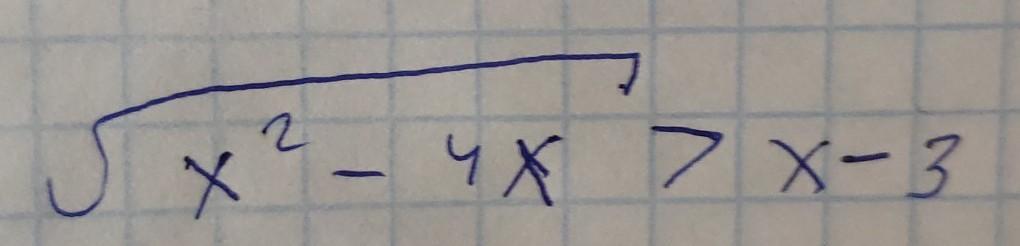
Ответы
Автор ответа:
0
Ответ:
x є (4+1/2;+бесконечность).
От четырёх целых одна вторая до бесконечности.
Пошаговое объяснение:
В неравенствах нельзя делать через проверку. Здесь всегда должно быть ОДЗ.
ОДЗ:
bodikivchenko:
так ОДЗ от 4 до +бесконечности?
нет там +-+
подставь +бесконечность
ОДЗ от -бесконечности до 0 и от 4 до +бесконечности
в квадрат нельзя возводить
надо сказать что если х меньше 3 то неравенство очевидно и рассмотреть случай х больше или равно 3 и уже возводить в квадрат
Значит ответ будет от -бесконечности до 3 и от 4,5 до +бесконечности.
вроде так
от минус бесконечности до нуля, от 4,5 до + бесокнечности
++
Похожие вопросы
Предмет: Українська мова,
автор: dsfgsdfgsdfg
Предмет: Английский язык,
автор: baku009
Предмет: Українська мова,
автор: Аноним
Предмет: Обществознание,
автор: диана2194
Предмет: Биология,
автор: anna20032017