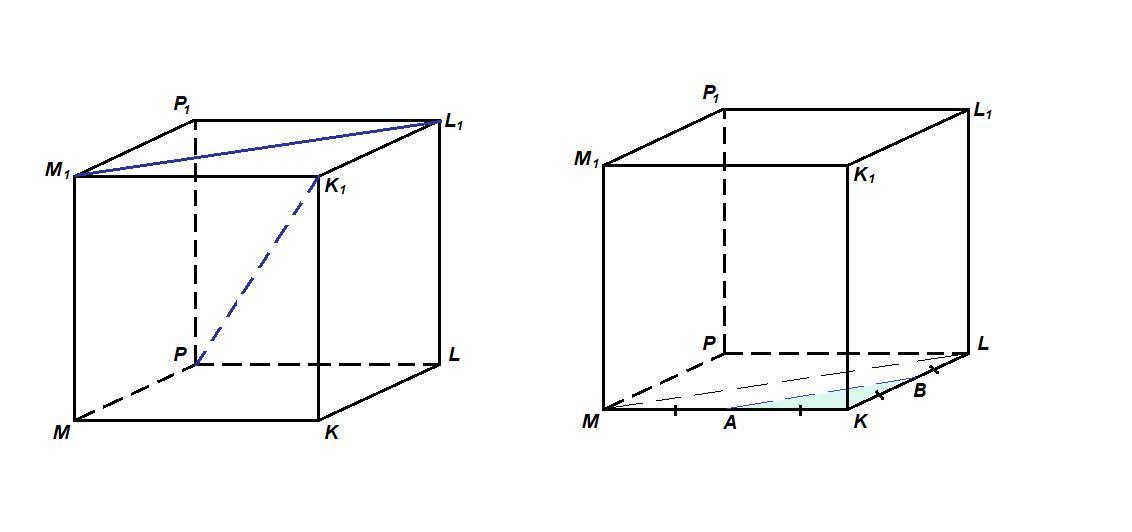
1. Выполните чертеж куба MKLPM1K1L1P1. По чертежу укажите:
а) прямые параллельные для прямой MK;
б) прямые скрещивающиеся с прямой LL1;
в) плоскости параллельные прямой PL.
Пересекаются ли прямые
K1P и KL?
K1P и M1L1?
KL линией пересечения каких плоскостей является
Найти:
3 пары параллельных прямых,
3 пары скрещивающихся прямых,
3 пары пересекающихся прямых.
Найти S∆MKL, а S∆AKB=8 где A – середина MK, B-середина KL
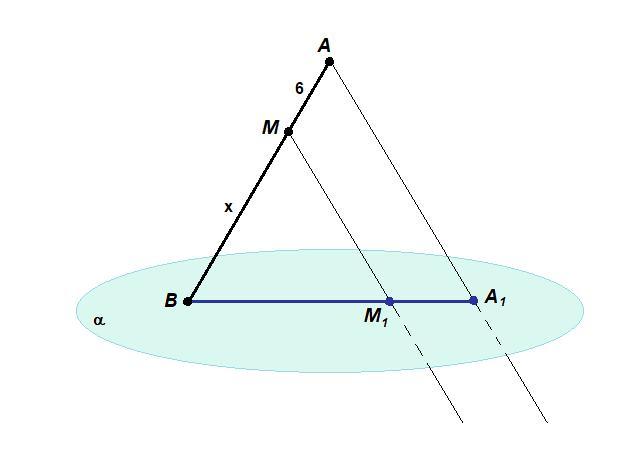
2. Точка М лежит на отрезке АВ. Отрезок АВ пересекается с плоскостью α в точке В. Через А и М проведены параллельные прямые, пересекающие α в точках А1 и M1.
а) Докажите, что А1, М1 и В лежат на одной прямой.
б) Найдите длину отрезка АВ, если АА1 : ММ1 = 3 : 2, AM = 6.
Ответы
Ответ:
1.
а) MK ║ PL ║ M₁K₁ ║ P₁L₁
б) прямые, скрещивающиеся (не лежащие в одной плоскости) с прямой LL₁:
МК, МР, МК₁, МР₁
в) PL ║ (MM₁K), PL ║ (M₁K₁P₁)
________
Прямые К₁Р и KL не пересекаются.
Прямые К₁Р и M₁L₁ не пересекаются.
________
Прямая KL является линией пересечения плоскостей (МКL) и (KLL₁).
________
3 пары параллельных прямых:
MK ║ PL, MM₁ ║ KK₁, M₁P₁ ║ K₁L₁
3 пары скрещивающихся прямых:
МК и РР₁, МР и КК₁, PL и ММ₁
3 пары пересекающихся прямых:
МК ∩ МР = М, РР₁ ∩ PL = P, LL₁ ∩ LK = L
________
S_{ABK} = 8
А - середина МК, В - середина KL, значит АВ - средняя линия треугольника MKL.
Средняя линия треугольника отсекает треугольник, подобный данному с коэффициентом подобия k = 1/2. Значит,
ΔАКВ ~ ΔMKL
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
2.
а) Через две пересекающиеся прямые АВ и АА₁ проходит плоскость (АА₁В). Прямая АВ лежит в этой плоскости, значит и точка М так же лежит в ней.
В этой плоскости через точку М можно провести единственную прямую, параллельную прямой АА₁. Значит, прямая ММ₁ лежит в плоскости (АА₁В).
Плоскость (АА₁В) пересекает плоскость α по прямой ВА₁, на которой лежат все их общие точки, значит и точка М₁.
Итак, точки А₁, М₁ и В лежат на одной прямой.
б) АА₁ : ММ₁ = 3 : 2
В треугольнике АВА₁ проведена прямая ММ₁, параллельная стороне АА₁, значит она отсекает треугольник, подобный данному.
ΔВММ₁ ~ ΔВАА₁
Пусть ВМ = х, тогда
АВ = ВМ + МА = х + 6
3x = 2(x + 6)
3x = 2x + 12
x = 12
AB = 12 + 6 = 18