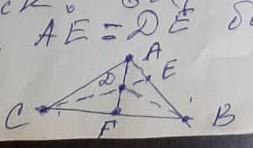
Дано BF=CF=BD.
Доказать что АЕ=ДЕ
Ответы
Ответ: ну почему же "невероятно"...
если построить рисунок по условию, то даже похоже, что и AE=DE...
Объяснение:
треугольник BDF по условию равнобедренный...
и, если начать построение именно с этого, вполне себе получится адекватный рисунок))
т.к. BF=CF по условию ---> AF; CE -медианы и BD -тоже часть медианы...
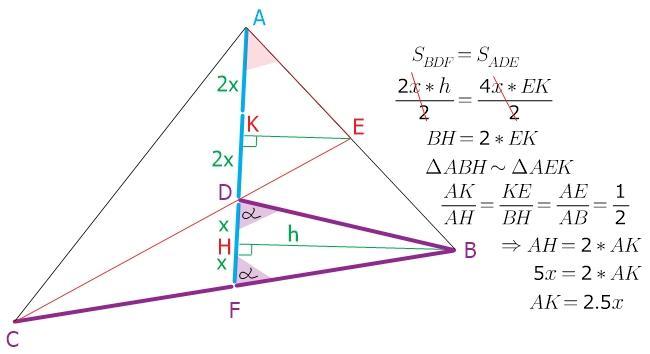
AE=BE и доказать, что AE=BE=DE -такое возможно только в прямоугольном треугольнике))) нужно смотреть углы...
а вот треугольник ADB уже не очень похож на прямоугольный...
медианы точкой пересечения делятся в отношении 2:1, считая от вершины.
CD=2*DE; AD=2*DF
медианы делят треугольник на шесть равновеликих треугольников.
S(ADE) = S(BDF) = S(BDE) = S(CDF)...
у меня не получилось, что треугольник ADE-равнобедренный)))
либо точнее условие, либо в моих рассуждениях есть ошибка...
требуется доказать, что AE=DE, т.е. высота ЕК будет и медианой
---> АК = DK = 2х должно быть...