Предмет: Математика,
автор: draidforyoufor
Математика 10 класс
Даю балов по максималки при решении всего! (И 1, и 2-го и всего)
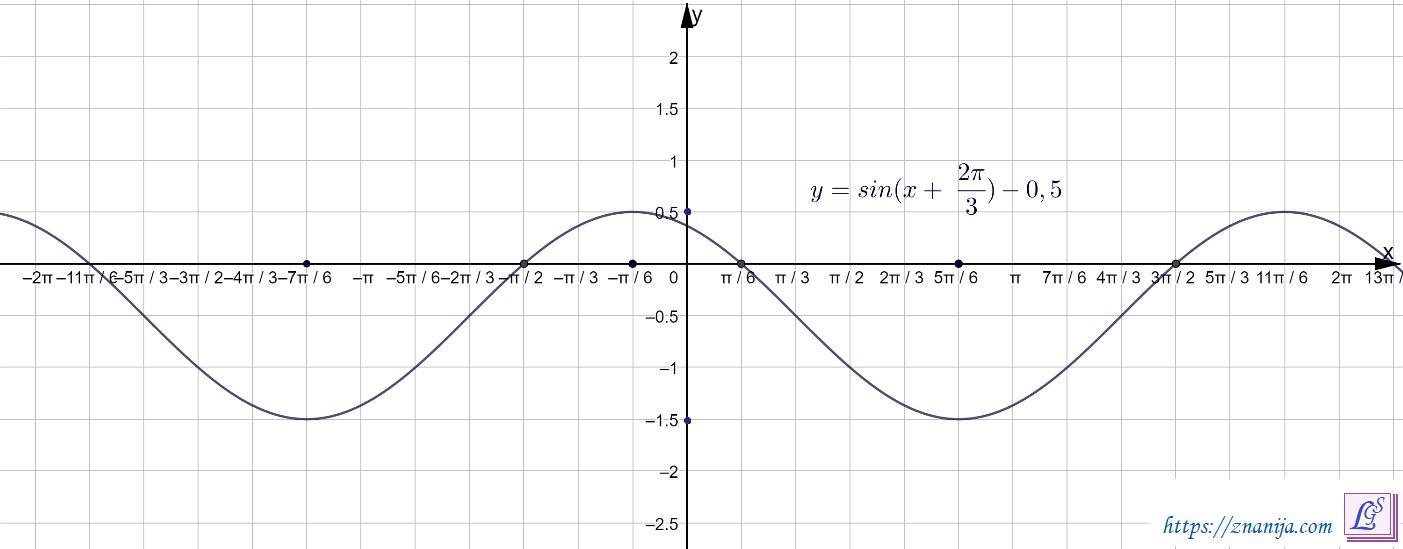
Сама функция: y=sin(x+ )-0,5
)-0,5
Приложения:

Ответы
Автор ответа:
3
Ответ:
График функции получается сдвигом графика
вдоль оси OX на
единиц и вдоль оси OY на -0,5 единиц.
Свойства функции .
1) Область определения функции x ∈ (-∞; +∞).
2) Область значений функции y ∈ [-1,5; 0,5].
3) Периодичность. Функция периодическая с периодом T = 2π.
4) Четность функции не определенная (не является четной, не является нечетной).
5) Нули функции.
y = 0 при и
Решение
6) а) Наибольшее значение функции y = 0,5 при
б) Наименьшее значение функции y = -1,5 при
7) а) Функция убывает при
б) Функция возрастает при
8) Промежутки знакопостоянства
y > 0 при
y < 0 при
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: annaka366
Предмет: Русский язык,
автор: lowep
Предмет: Українська мова,
автор: dmitruk8
Предмет: Химия,
автор: Svet2003a
Предмет: Алгебра,
автор: назар157