Предмет: Математика,
автор: mariyanar
помогите с решением!!!!!!!!!!!!!!!
Приложения:
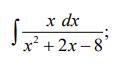
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Методом неопределённых коэффициентов:
=
mariyanar:
Верхняя картинка не доступна, поэтому не могу понять как вы к этому перешли и куда делся х в числителе)
нашла информацию про неопределённые коэффициенты, спасибо
сейчас видно?
да)
Похожие вопросы
Предмет: Русский язык,
автор: zhenya22096
Предмет: Русский язык,
автор: 5i573m3rr0r
Предмет: Русский язык,
автор: shutkomatvey
Предмет: Геометрия,
автор: sandra106
Предмет: Биология,
автор: yrrrrtt