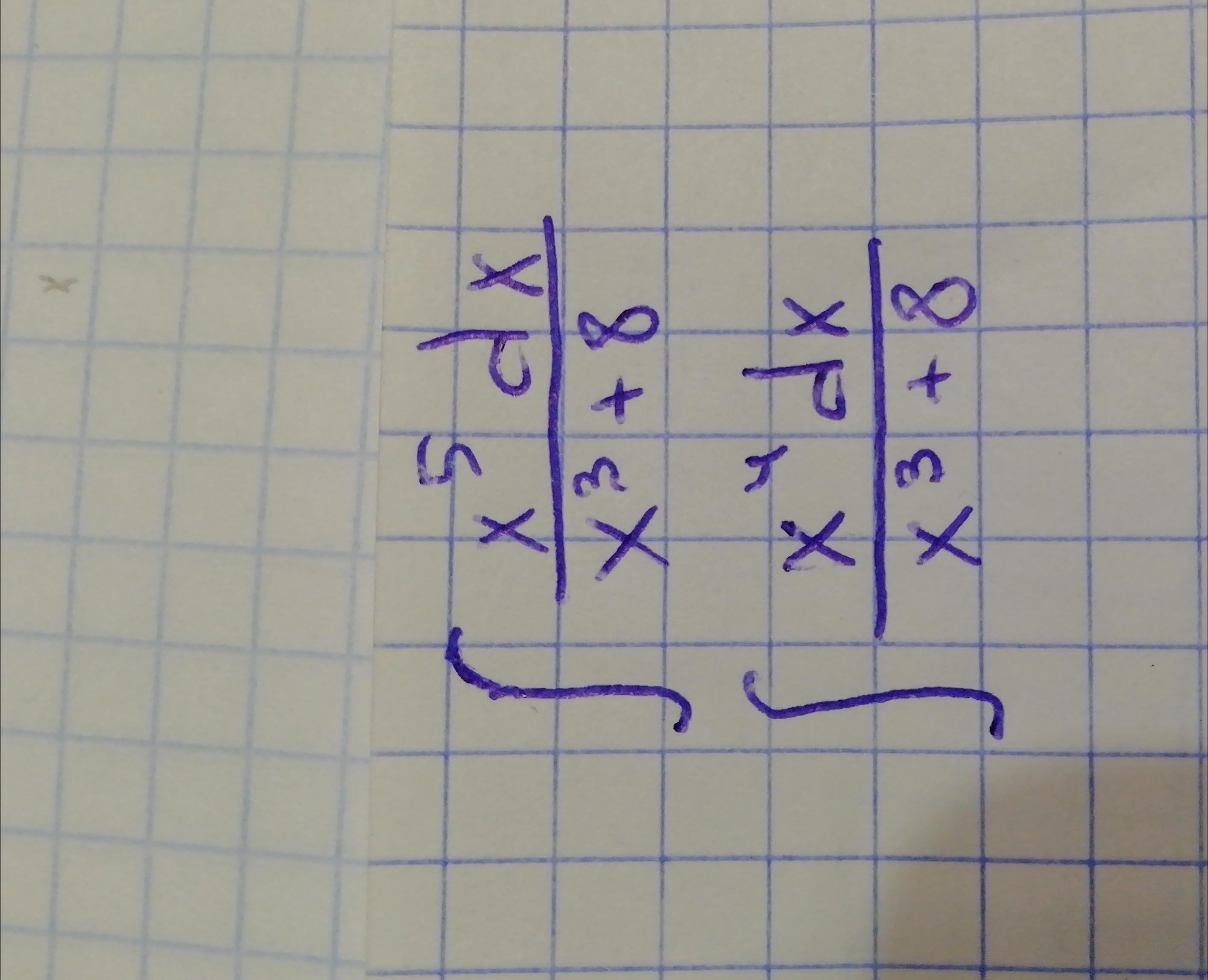
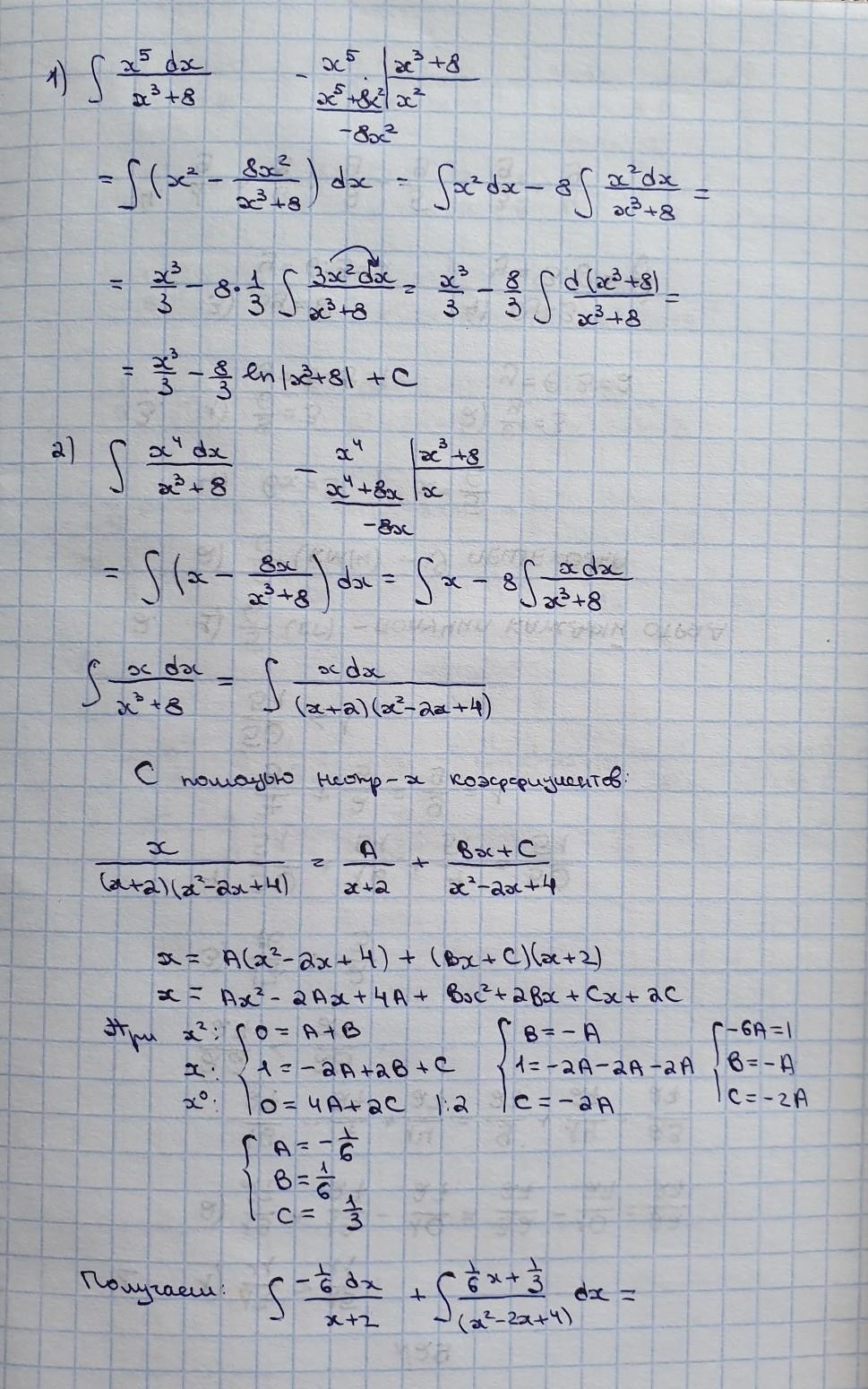Чем отличаются эти интегралы? (И не надо говорить, что степенью числителя)
Почему один нужно решать методом подстановки, а второй как простую рациональную дробь?
И, если возможно, то решение бы тоже не помешало... Особенно первого.
Ответы
Ответ:
оба эти интеграла содержат неправильную дробь (старшая степень х в числителе больше старшей степени х в знаменателе). Но когда выделяем целую часть, видим, что решаются они по-разному. Тут нет какого-то чёткого объяснения, почему именно так, просто с практикой сразу видишь.
в первом раскладываем и получаем х^2 как целую часть и 8х^2 - остаток, остаётся в дроби. Далее видно, что этот числитель можно легко домножить на число и занести под знак дифференциала, тогда интеграл легко возьмётся. (x^3+8)'=3x^2, соответственно домножаем x^2 на 3 (1/3 и 8 остаются за знаком интеграла) и заносим в дифференциал. И все, интегрируем это выражение как одну переменную по формуле: интеграл от 1/а = ln(a) + C. Можно сделать замену, но думаю, что легче так, как сделала я.
Во втором уже не все так просто. Выделяем целую часть и получаем х в числителе. По-другому, кроме как разложением на более простые дроби, уже не решить. С помощью неопр. коэф-в раскладываем, получаем две дроби, решаем по отдельности. С первой дробью все просто, получаем логарифм, со второй проделываем ту же манипуляцию, что и в 1м интервале. берем произврдную знаменатель (x^2-2x+4)'=2x-2, и делаем ее в числителе, то есть домножаем его на 2 (получили 2х+4), и раскладываем 4 как -2+6. Делим почленно и снова получаем две дроби. В первом снова заносим под дифференциал и получаем логарифм, а во втором в знаменателе нужно выделить квадрат, чтобы интегрировать по одной из табличных формул (arctg в нашем случае).