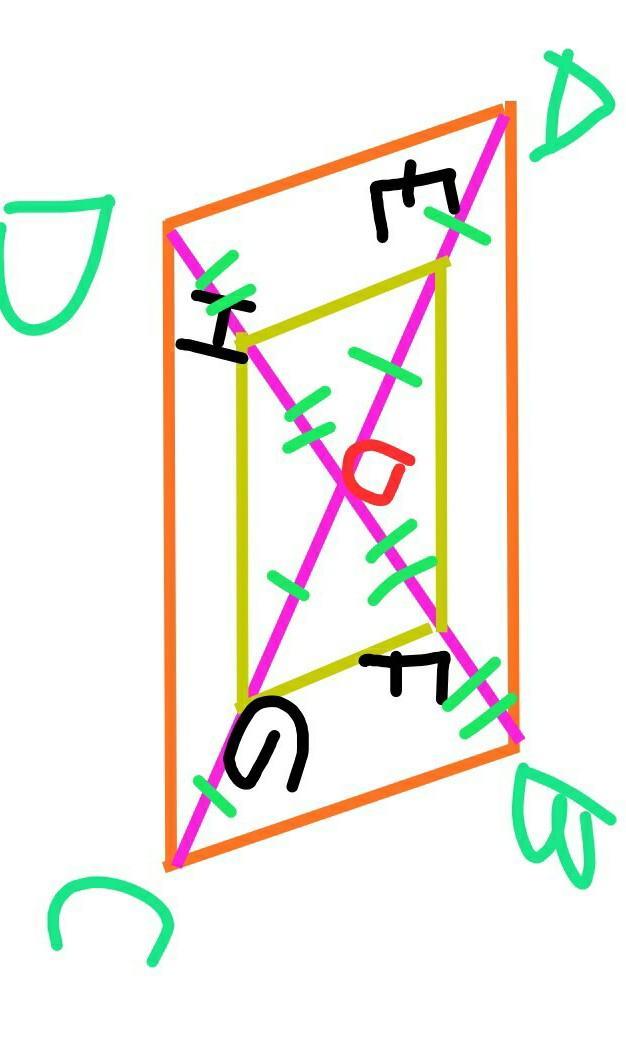
в параллелограмме ABCD диагонали пересекаются в точке о. Докажите что четырехугольник EFGH вершинами которого является середины отрезков AO,OB,OC и OD - параллелограмм. ПРОШУ ЛЮДИ, ХЕЛП!!!!
Ответы
Ответ:
здесь нужно вспомнить про подобие треугольников:
★ Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.
Рассмотрим треугольники АВО и EFO.
Сторона EO это половина стороны АО соответственно эти стороны пропорциональны.
Сторона FO это половина стороны ВО значит эти стороны тоже пропорциональны.
Угол АОВ и угол EOF это один и тот же угол.
Из выше написанного делаем вывод что треугольники ABO и EFO подобны.
По тому же самому принципу доказываем подобие треугольников DOC и HOG.
Так как треугольники АВО и DOC равны то соответственно и треугольники EFO и HOG тоже равны, а значит стороны EF и HG равны.
Точно таким же методом доказываем равенство сторон EH и FG.
Теперь вспомним про подобие многоугольников:
★Два многоугольника называются подобными, если углы одного равны попарно углам другого и если сходственные стороны их пропорциональны.
Так как мы доказали что треугольники многоугольника EFGH подобны треугольниками параллелограмма ABCD мы модем доказать равенство углов.
Таким образом сумма углов HEO и OEF равна сумме углов DAO и OAB. А это значит что углы DAB и HEF равны.
Таким же образом доказываем равенство всех остальных углов.
Имея все данные мы можем доказать что многоугольник EFGH подобен многоугольнику ABCD:
стороны EF и AB а также HG и DC исходя из подобия треугольников пропорциональны;
стороны EH и ADа также FG и BC исходя из подобия треугольников пропорциональны;
так же мы доказали что углы многоугольников тоже попарно равны.
делаем вывод: многоугольник EFGH подобен многоугольнику ABCD!
а так как ABCD - это параллелограмм, то значит и EFGH тоже параллелограмм!