Предмет: Алгебра,
автор: KASDROM
Найти неопределенные и определённые интегралы.
Приложения:
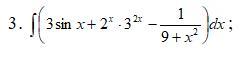

Ответы
Автор ответа:
1
Ответ:
Объяснение:
KASDROM:
Я тебя люблю.Ты мой спаситель.
Как тебе все баллы отдать?
Так я вроде все получил.
Та просто.Эти примеры надо решить до завтра.Если бы не ты,мне бы 2 поставили в меде.
В меде значит на медицинском?
Да.
Похожие вопросы
Предмет: Русский язык,
автор: dmitriytsios
Предмет: Русский язык,
автор: zalik5529
Предмет: Русский язык,
автор: shevyrevae
Предмет: Биология,
автор: MadLiz