Предмет: Алгебра,
автор: 381727c39be5
Найти значение выражения сократив его
Приложения:
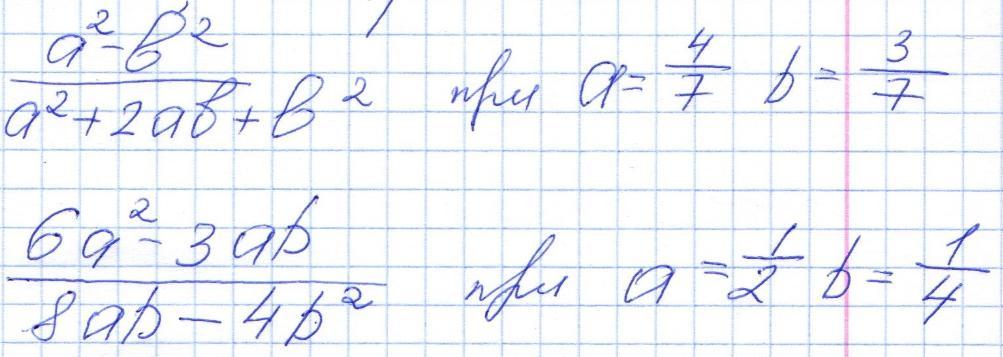
Ответы
Автор ответа:
2
Ответ:
(a-b)(a+b)/(a+b)² = 1/7
3a(2a-b)/4b(2a-b)= 1.5
Объяснение:
(a-b)(a+b)/(a+b)²=(a-b)/(a+b)=(4/7-3/7)/(4/7+3/7)=1/7
3a(2a-b)/4b(2a-b)=3a/4b=3*1/2/4*1/4=1.5
381727c39be5:
хорош
спасибо
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: olyaveber
Предмет: Русский язык,
автор: Nukuma190
Предмет: Русский язык,
автор: svetuliy112
Предмет: Алгебра,
автор: остстат