Предмет: Геометрия,
автор: liza2004che
ПОМОГИТЕ ПОЖАЛУЙСТА!!!!!!!!
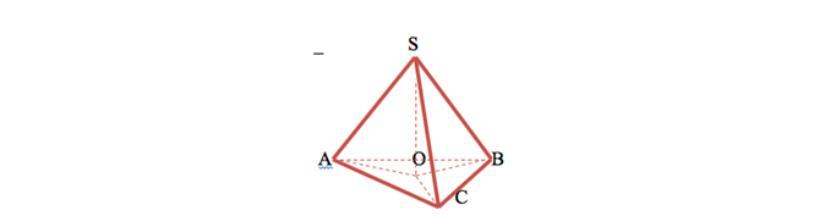
Дано: пирамида SABC, SO = высота, SA = SB= SC= AB= AC = CB = a.
Найти: SO
Приложения:
Аноним:
Найти высоту треугольника. По формуле h=a√3/2. Пересечение медиан делится в отношении 2:1 от вершины. Умножаем на 2/3. ОА=а√3*2/2*3=а/√3. Теорема Пифагора SO=√(SA²-AO²)=√(a²-a²/3)=√(2a²/3)
Ответы
Автор ответа:
6
Ответ:
SO =
Объяснение:
По условию видно, что пирамида правильная, а значит в основании пирамиды лежит равносторонний треугольник
Высота в нём будет равна по т. Пифагора:
Высоты равностороннего треугольника являются медианами и делятся в отношении 2:1, считая от вершины
Получается АО=ВО=СО=
Рассмотрим ΔSAO
по т. Пифагора:
SO = √(AS²-AO²)
SO =
Похожие вопросы
Предмет: Русский язык,
автор: nata852010
Предмет: Русский язык,
автор: LizaTa1
Предмет: Русский язык,
автор: 6alinaoar
Предмет: Физика,
автор: zhamillia