Предмет: Геометрия,
автор: Оля199605
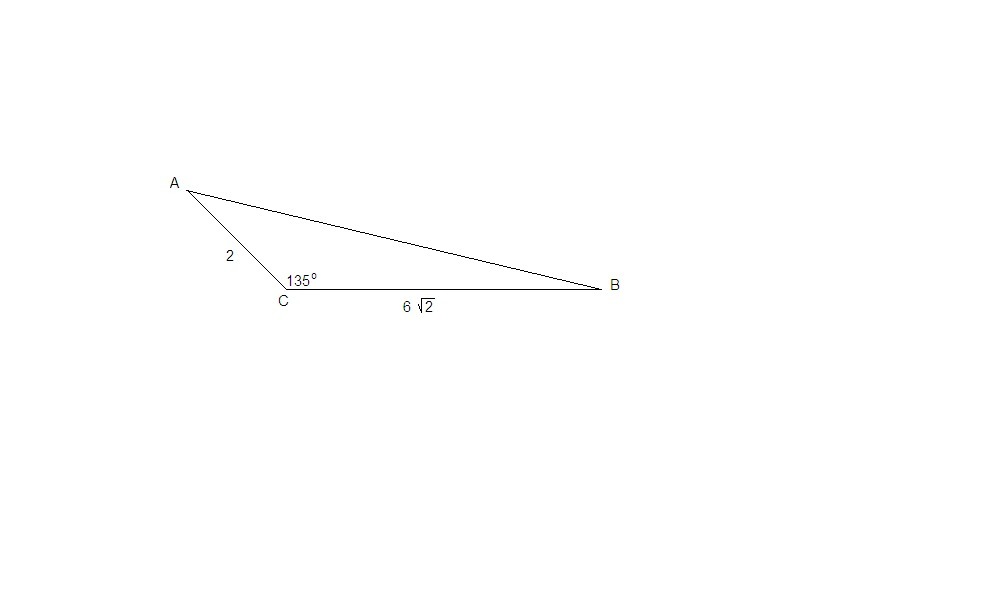
решите треугольник АВС если ВС=6 корней из 2, АС=2, угол=135 градусов
Ответы
Автор ответа:
0
ВС = 6√2, АС = 2, ∠С = 135°.
cos 135° = - cos 45° = - √2/2
По теореме косинусов:
АВ² = AC² + BC² - 2·AC·BC·cosC
AB² = 4 + 72 - 2 · 2 · 6√2 · (- √2/2) = 76 + 24 = 100
AB = 10
По теореме синусов:
AB : sin C = AC : sin B
sin B = AC · sin C / AB = 2 · sin 135° / 10 ≈ 0,7071 / 5 ≈ 0,1414
∠B ≈ 8°
Так как сумма углов треугольника 180°:
∠А = 180° - (∠С + ∠В) ≈ 180° - (135° + 8°) ≈ 37°
cos 135° = - cos 45° = - √2/2
По теореме косинусов:
АВ² = AC² + BC² - 2·AC·BC·cosC
AB² = 4 + 72 - 2 · 2 · 6√2 · (- √2/2) = 76 + 24 = 100
AB = 10
По теореме синусов:
AB : sin C = AC : sin B
sin B = AC · sin C / AB = 2 · sin 135° / 10 ≈ 0,7071 / 5 ≈ 0,1414
∠B ≈ 8°
Так как сумма углов треугольника 180°:
∠А = 180° - (∠С + ∠В) ≈ 180° - (135° + 8°) ≈ 37°
Приложения:
Похожие вопросы
Предмет: Информатика,
автор: zulhatamangalieva
Предмет: Окружающий мир,
автор: madiarbaglanuly130
Предмет: Математика,
автор: aminamasaripova0
Предмет: Алгебра,
автор: Nastenka0611