Предмет: Алгебра,
автор: zubkovadoc
Пожалуйста, помогите! Желательно не просто ответ, а объяснение как и почему так решается. Или хотя бы просто поэтапно расписать решение.
Докажите, что при всех допустимых значениях переменных значение выражения не зависит от значения переменных:
Приложения:
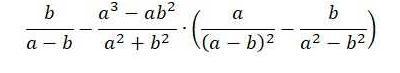
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Другие предметы,
автор: marial800
Предмет: Английский язык,
автор: maks200099
Предмет: Українська мова,
автор: Fox2701
Предмет: Алгебра,
автор: Valdys9