Question

Здравствуйте, помогите пожалуйста
${x}^{11} + {x}^{3} = 2$



$2x {}^{4} + {x}^{10} = 3$
​

Answer 1

$1)\ \ x^{11}+x^3=2$

Функция  $y=x^{11}+x^2$   является нечётной , возрастающей . Может пересекаться с постоянной функцией  $y=2$  только один раз . Подбором определяем , что при х=1:  $1^{11}+1^3=1+1=2$ .

Значит решением уравнения является  $x=1\ .$

$2)\ \ 2x^4+x^{10}=3$

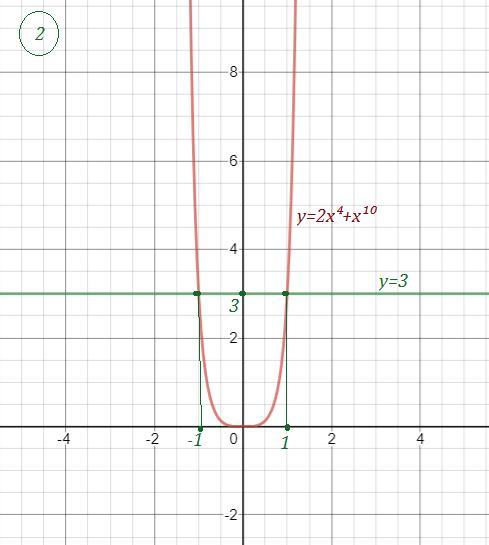
Функция  $y=2x^4+x^{10}$     является чётной, значит её график симметричен относительно оси ОУ и при пересечение с графиком постоянной функции  $y=3$  будет в двух симметричных точках . Это точки с абсциссами  х=1 и х= -1 .

Значит решением уравнения являются $x=1\ ,\ x=-1\ .$

Answer 2

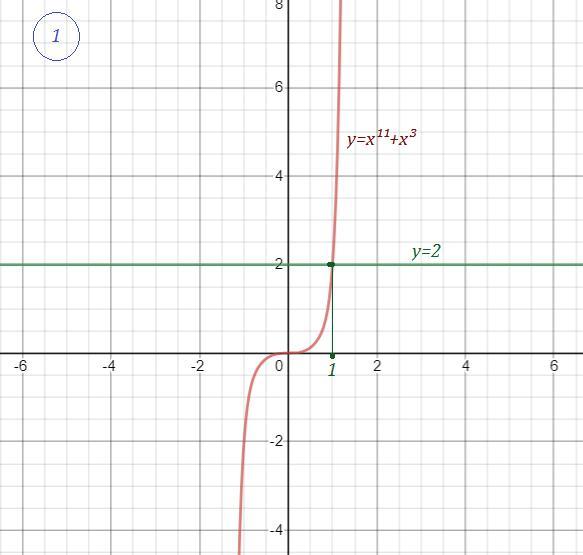
1. х¹¹=2-х³

слева возрастающая во всей области определения функция, справа убывающая. поэтому, если есть корень у уравнения. то он только один. и находится путем  подбора.  х=1

Ответ 1

2. 2х⁴=3-х¹⁰

а) при х больше или равно нулю слева возрастающая, справа убывающая, если есть корень. то он один. и этот корень х=1

б) при х меньше нуля (или равно нулю)

слева убывающая, справа возрастающая функция. поэтому если есть корень. то он только один. этот корень х=-1

Ответ ±1