Предмет: Алгебра,
автор: Daeir
Помогите, пожалуйста с решением! Даю 100 баллов! Дети(а может и взрослые), которые напишут ерунду ради баллов, убедительная просьба - не делайте так. Баллов мне не жалко, но вопрос тонет и я не могу разобраться в своей проблеме. Спасибо!
Приложения:

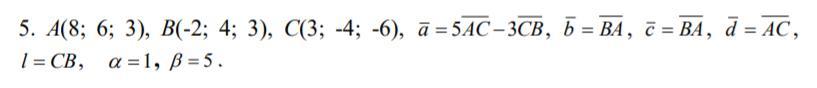
Ответы
Автор ответа:
0
Daeir:
Сделано просто прекрасно! Но вы по-моему ошиблись в расчетах: вектор а = 5ас-3св и там получается -25+15, а не -26, отсюда дальше неправильно.
Похожие вопросы
Предмет: Русский язык,
автор: dimakrailocom
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: jinbion15
Предмет: История,
автор: elendaayan
Предмет: Литература,
автор: edgorovav