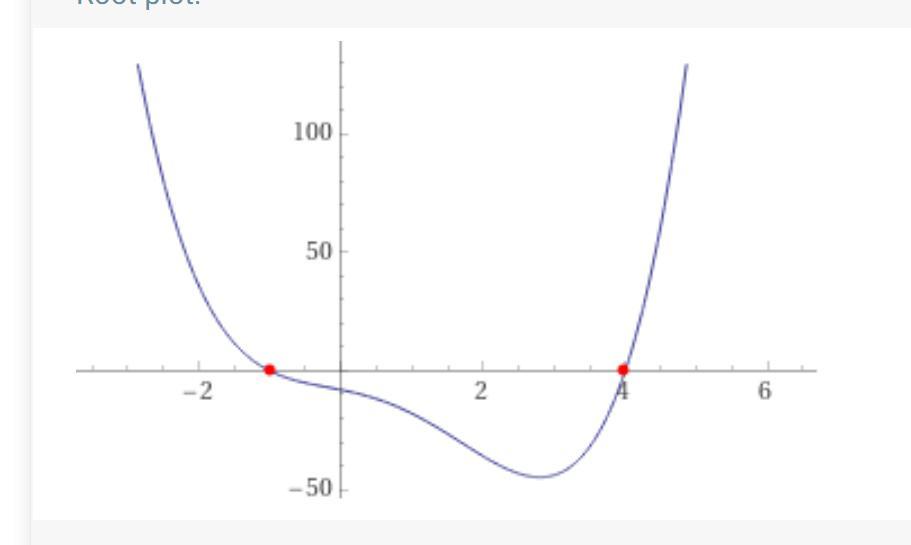
Помогите решить уравнение x^4-3x^3-2x^2-6x-8=0. Плачу 25 баллов.
Ответы
Корень уравнения бывает среди множителей свободного члена.
Это +-1, +-2, +-4 и +-8.
Подходит х = -1. Проверяем:
(-1)^4 - 3*(-1)^3 - 2*(-1)^2-6*(-1)-8 = 1 +3 - 2+ 6 - 8 = 0.
Делим заданный многочлен x^4-3x^3-2x^2-6x-8 на (х + 1).
x^4-3x^3-2x^2-6x-8 | x + 1
x^4+x^3 x^3 - 4x^2 + 2x - 8
-4x^3-2x^2
-4x^3-4x^2
2x^2-6x
2x^2+2x
-8x-8
-8x-8
0
Получаем x^4-3x^3-2x^2-6x-8 = (x + 1)(x^3 - 4x^2 + 2x - 8) = 0.
Так же находим корень кубического трёхчлена среди множителей его свободного члена. Это х = 4.
Проверяем: 4^3 - 4*4^2 + 2*4 - 8 = 64 - 64 + 8 - 8 = 0.
Делим x^3 - 4x^2 + 2x - 8 на (х - 4).
x^3 - 4x^2 + 2x - 8 | x - 4
x^3 - 4x^2 x^2 + 2
2x - 8
2x - 8
0
Получили разложение исходного многочлена:
x^4-3x^3-2x^2-6x-8 = (x + 1)(x + 4)(x^2 + 2) = 0.
Так как последний множитель не имеет корней, то остаются 2 найденных.
Ответ: х1 = -1, х2 = 4.