Question

07.10.2020
Суммативное оценивание за раздел
«Уравнения, неравенства с двумя переменными и их системы»

Answer 1

Номер 1

{x + 4у = 8

{2х - 4у = 4

{4y = 8 - x

{2x - 4y = 4

2x - (8 - x) = 4

2x - 8 + x = 4

3x = 12

x = 4

Можно подставить Х в начальную систему уравнения:

4 + 4у = 8

4у = 4

у = 1

Номер 2

{(x + 3)^2 + (y - 1)^2 = 9

{y = -2

(x + 3)^2 + (-2 - 1)^2 = 9

(x + 3)^2 + 9 = 9

x^2 + 3^2 = 0

Результатом возведения в степень может быть 0, только тогда, когда основание равно 0

х + 3 = 0

х = -3

у = -2

Номер 3

х - 1 число

х + 5 - 2 число. х є N

х × (х + 5) = 36

х^2 + 5х = 36

х^2 + 5х - 36 = 0

х^2 + 9х - 4х - 36 = 0

х × (х + 9) - 4 × (х + 9) = 0

(х + 9) × (х - 4) = 0

{х + 9 = 0

{х - 4 = 0

{х = -9

{х = -4

То есть первое число -9, а второе число -4

Сумма: -4 + (-9) = -4 -9 = -13

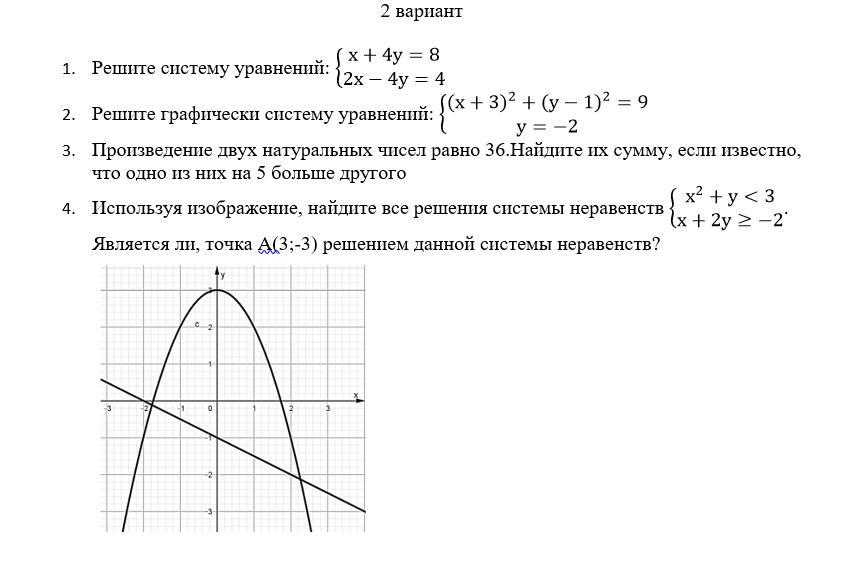
Номер 4