Предмет: Математика,
автор: kira100088
Случайная величина ξ задана функцией F(x) распределения вероятностей:
Найти плотность вероятности и числовые характеристики этой случайной величины.
Приложения:
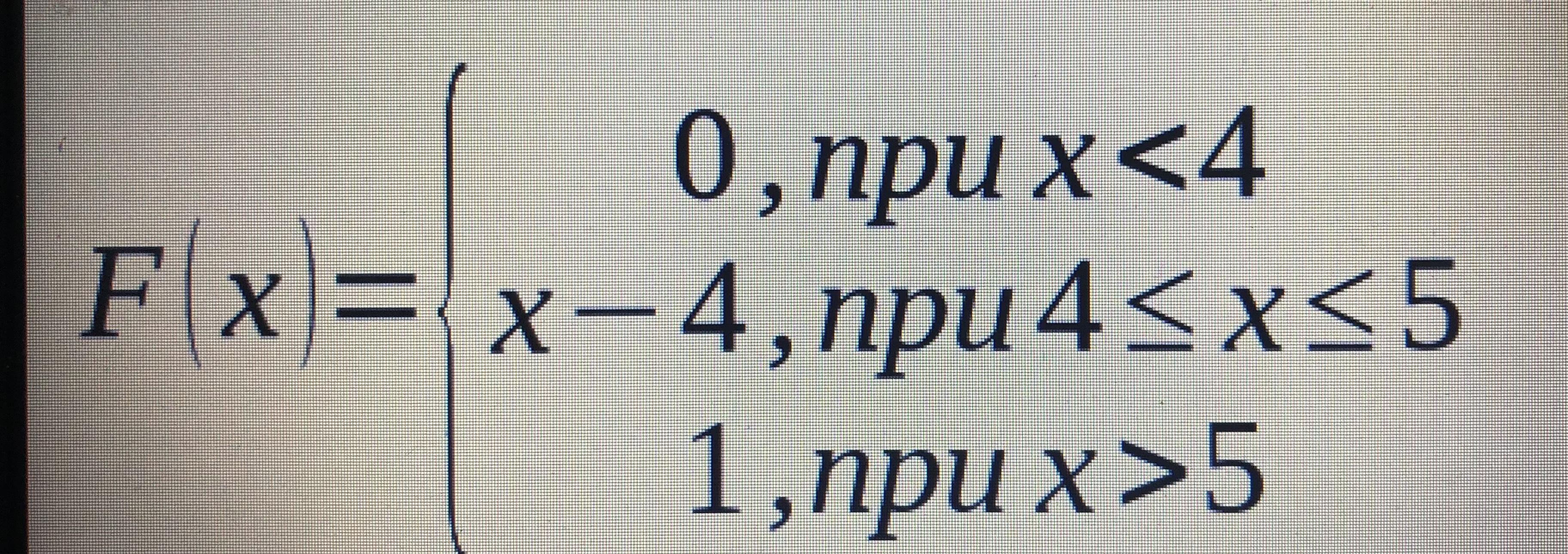
Ответы
Автор ответа:
4
Запишу правильное оформление функции распределения и дополню, что случайная величина является непрерывной.
Задана функция распределения .
Плотность вероятности распределения будем искать как производную от функции распределения
Найти числовые характеристики этой случайной величины означает, что нужно определить математическое ожидание, дисперсию и среднеквадратическое отклонение этой величины
Похожие вопросы
Предмет: Русский язык,
автор: aik851
Предмет: Английский язык,
автор: 04kostenkouly
Предмет: Русский язык,
автор: ivanaivanova91
Предмет: Обществознание,
автор: ленура21
Предмет: Физика,
автор: Ym000