Предмет: Математика,
автор: ИэнШоу
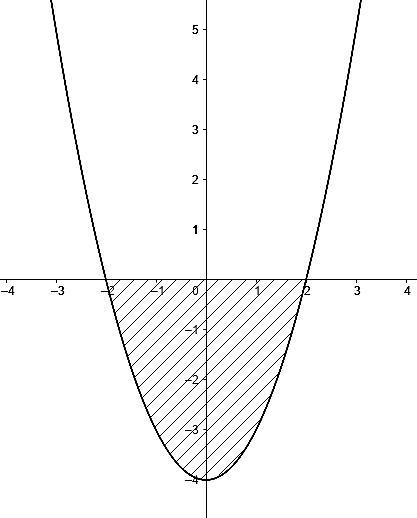
помогите вычислить при помощи определённого интеграла площадь фигуры, ограниченной графиком функции y=x^2-4 и осью Ox ;
C рисунком
Ответы
Автор ответа:
0
Для начала найдём значения х, при которых функция ограничена этими линиями, положив у = 0.
x² - 4 = 0
x = ± 2.
На рисунке площадь заштрихованной фигуры.
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: lina1987
Предмет: Русский язык,
автор: katerinagagarin
Предмет: Русский язык,
автор: oficerovavalenti
Предмет: Математика,
автор: Тима22876