Предмет: Алгебра,
автор: sqaaa
Преобразования выражений, содержащих квадратные корни. Урок 3
Освободи от иррациональности знаменатель дроби:
Приложения:
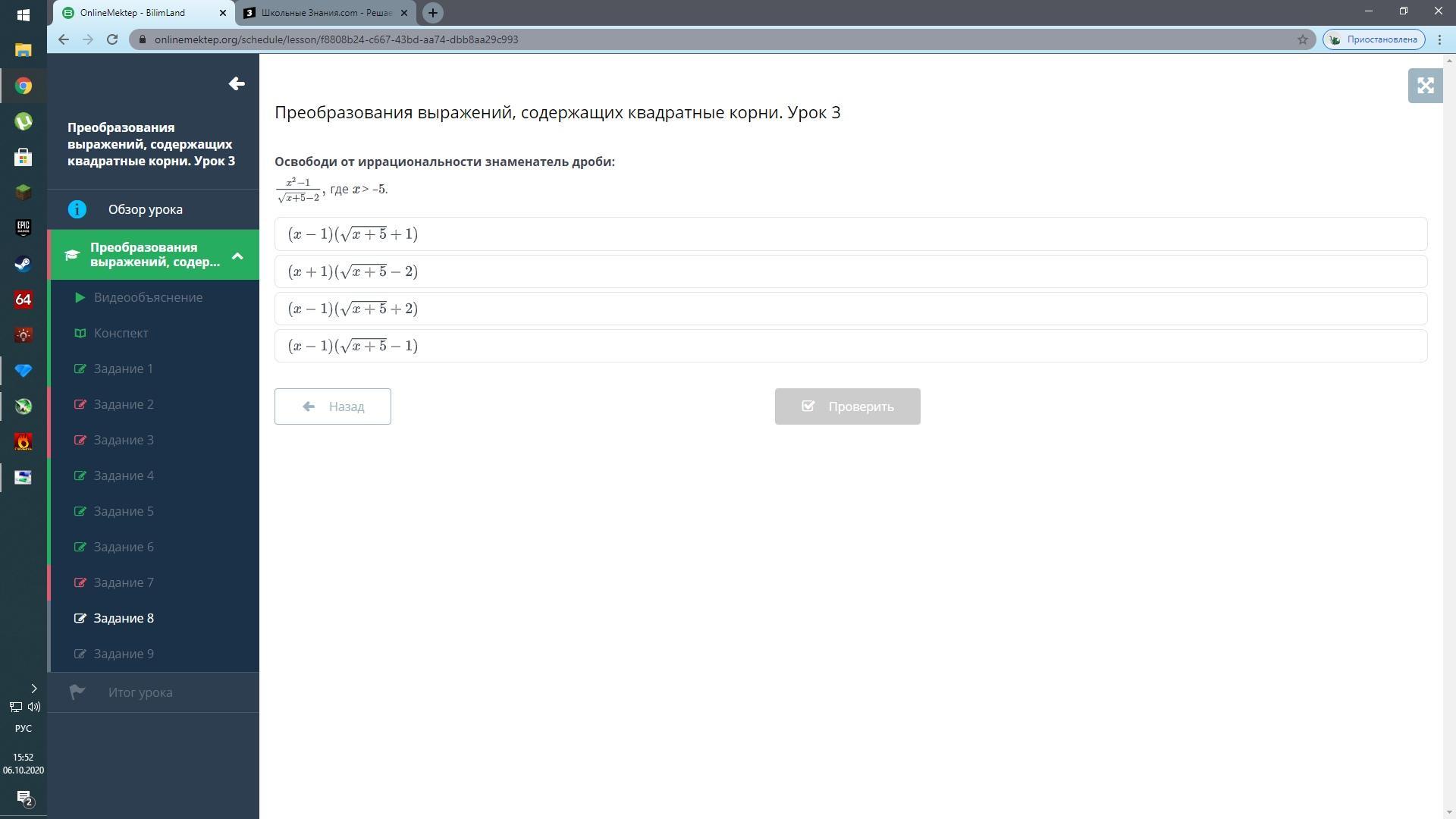
Ответы
Автор ответа:
3
Ответ:
Объяснение:
Требуется освободит от иррациональности знаменатель дроби:
Так как при x = -1 > -5 знаменатель дроби обращается в 0, добавим условие: x ≠ -1.
Используя основное свойство дробей числитель и знаменатель дроби умножим на одно и тоже выражение :
Далее, применив формулу сокращённого умножения (a-b)·(a+b)=a²-b² упростим дробь:
Похожие вопросы
Предмет: Русский язык,
автор: ulgreen08092002
Предмет: Русский язык,
автор: lida1948lida
Предмет: Русский язык,
автор: nasta8295
Предмет: Математика,
автор: МамедоваДуня1