Предмет: Алгебра,
автор: aldabergenovajamila
4sin²x + sin2x=3 как решить
Ответы
Автор ответа:
1
Ответ:
Объяснение:
!!!!!!!!!!!!!!!!!!!!!!!
Приложения:
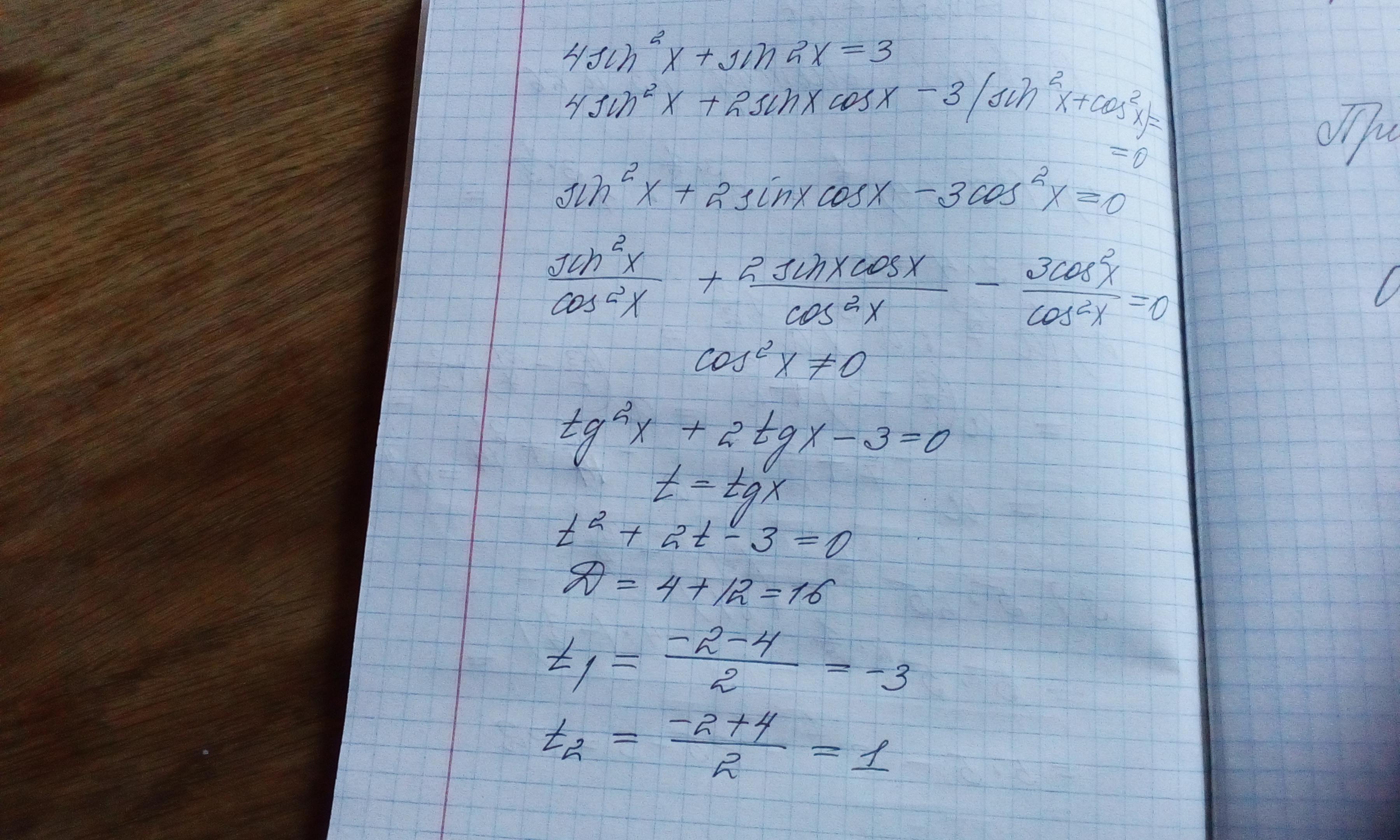

Автор ответа:
2
Ответ:
Получили две серии решений
1) .
2) .
Объяснение:
4sin²x+sin2x=3
По формуле двойного угла
sin2x=2sinxcosx преобразуем левую часть
4sin²x+2sinxcosx=3
Разделим обе части на cos²x.
По формуле
преобразуем левую часть.
Замена .
t²+2t-3=0
(t+3)(t-1)=0
t₁=-3; t₂=1.
1)
Так как арктангенс - нечетная функция, то решение можно записать в виде
.
2)
.
Похожие вопросы
Предмет: Английский язык,
автор: NatashaGryaznow
Предмет: Русский язык,
автор: nokrina
Предмет: Русский язык,
автор: АлиНчиk
Предмет: Алгебра,
автор: Приветприветпривет11
Предмет: Биология,
автор: Nikita2218876