Предмет: Геометрия,
автор: nikfantom199971
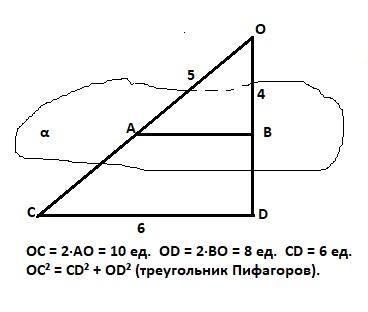
Плоскость α пересекает стороны OC и OD треугольника COD в точках A и B соответственно, и делит эти стороны пополам. Известно, что AO = 5, BO = 4 и CD = 6. Определи площадь треугольника COD.
Ответы
Автор ответа:
3
Ответ:
Площадь треугольника СОD равна 24 ед².
Объяснение:
Плоскость пересекает треугольник COD по средней линии, делящей стороны ОС и OD пополам. Следовательно, ОС = АО·2 = 10ед и ОD = ВО·2 = 8 ед.
Стороны треугольника СОD равны 6, 8 и 10 ед. Следовательно, это пифагоров треугольник с катетами CD и OD и гипотенузой CD.
Площадь прямоугольного треугольника равна половине произведения его катетов, то есть (CD·OD)/2 = 6·8/2 = 24 ед².
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: asl2323
Предмет: Русский язык,
автор: Super2321
Предмет: Русский язык,
автор: galihkamaslova
Предмет: Физика,
автор: mrsira08
Предмет: Математика,
автор: sobachka0504