Друга вправа! 2.Знайти точку, симетричну точці М...
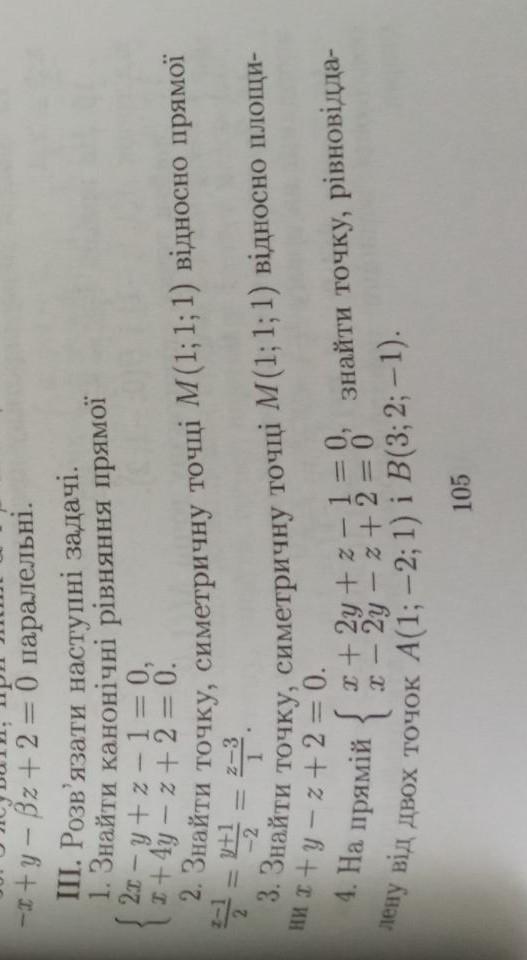
Ответы
Найти точку М1, симметричную точке М(1; 1; 1) относительно прямой.
(x-1)/2=(y+1)/(-2)=(z-3)/1.
Найдем уравнение плоскости, перпендикулярной прямой:
2(x-1)-2(y-1)+1(z-1),
2x - 2 - 2y + 2 + z - 1 = 0.
2x - 2y + z - 1 = 0.
Найдем точку Mo пересечения прямой и плоскости с использованием параметрического уравнения.
(x-1)/2=(y+1)/(-2)=(z-3)/1⇒
{(x=2t+1,
{y=-2t-1,
{z=t+3.) Подставим в уравнение плоскости.
4t+2+4t+2+t+3-1=0,
9t+6=0,
t=-6/9 = -2/3. Подставим эти значения в координаты точки пересечения с плоскостью.
{(x=2(-2/3)+1 = -1/3,
{y=-2(-2/3)-1 = 1/3,
{z=(-2/3)+3 = 7/3.
Mo=((-1/3); (1/3); (7/3))- координаты точки пересечения.
Отсюда,
x_Mo=(x_M+x_M1)/2⇒x_M1=2x_Mo-x_M=2*(-1/3)-1 = -5/3.
y_Mo=(y_M+y_M1)/2⇒y_M1=2y_Mo-y_M=2*(1/3)-1 = -1/3.
z_Mo=(z_M+z_M1)/2⇒z_M1=2z_Mo-z_M=2*(7/3)-1 = 11/3.
Следовательно, M_1 ((-5/3); (-1/3); (11/3)) - искомая точка.