Question

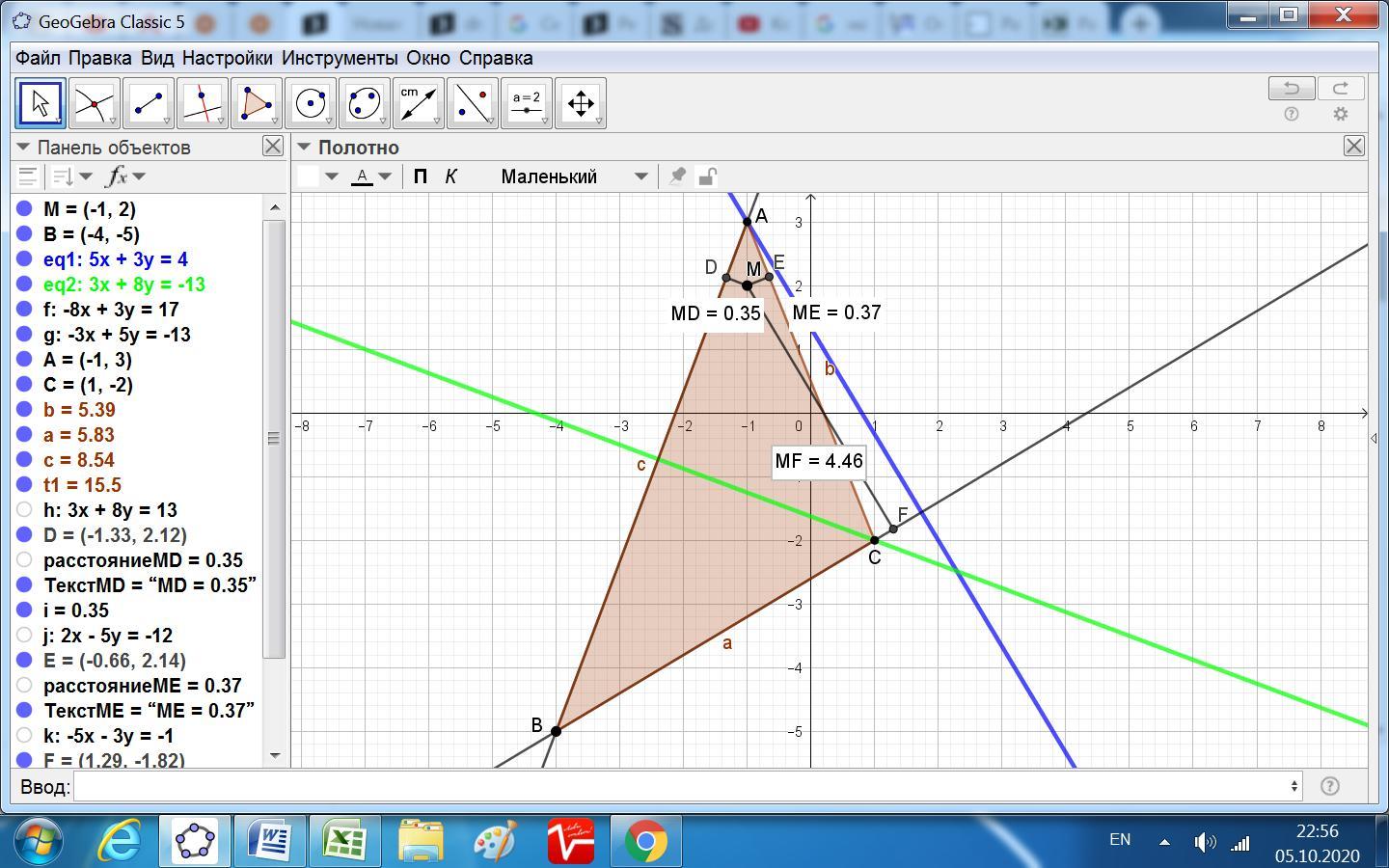
Знайти відстань від точки М (-1;2) до прямої L, а також кут між прямої L і площиною x+2y-z-4=0, якщо L є однією із сторін трикутника, для якого точка B(-4,-5) є вершиною, а прямі 5x+3y-4=0 і 3x+8y+13=0-висотами​

Answer 1

Решение к заданию 16).

Уравнения сторон как перпендикулярные высотам имеют вид:

h(BC): 5x + 3y - 4 = 0. Сторона ВС: -3х + 5у + С = 0.

Подставляем координаты точки В:

-3*(-4) + 5*(-5) + С = 0.

Находим С = 25 - 12 = 13.

Уравнение стороны ВС: -3х + 5у +13 = 0.

Аналогично получаем уравнение стороны АВ: -8х + 3у - 17 = 0.

Координаты вершин находим как точки пересечения сторон АВ и ВС с высотами.

-8х + 3у - 17 = 0.      -8х + 3у - 17 = 0.

5х + 3у - 4 = 0.       -5х - 3у + 4 = 0    

                               -13х       -13 = 0        х = 13/(-13) = -1.

у = (8*(-1) + 17)/3 = 9/3 = 3.

Точка А(-1; 3).

Аналогично находим координаты точки С(1; -2).

Вектор АС= (2; -5).

Уравнение стороны АС: (х + 1)/2 = (у - 3)/(-5)  это каноническое.

Или в общем виде 5х + 2у - 1 = 0.

Переходим к расстоянию от точки до прямой.

Для вычисления расстояния от точки M(Mx; My) до прямой Ax + By + C = 0 используем формулу:

d = |A•Mx + B•My + C| / √(A2 + B2).

Подставим в формулу данные точки М и прямой АВ:

d = |-8•(-1) + 3•2 + (-17)| / √((-8)2 + 32) = |8 + 6 - 17|√64 + 9 =

= 3/√73 = 3√73/73 ≈ 0.35112.

Подставим в формулу данные точки М и прямой АС:

d = |5•(-1) + 2•2 + (-1)| / √(52 + 22) = |-5 + 4 - 1|√25 + 4 =

= 2/√29 = 2√29/29 ≈ 0.37139.

Подставим в формулу данные точки М и прямой ВС:

d = |-3•(-1) + 5•2 + 13| / √((-3)2 + 52) = |3 + 10 + 13| / √(9 + 25) =

= 26√34 = 13√34/17 ≈ 4.45896.