Предмет: Алгебра,
автор: samoiluk04
ПОСТАВИЛ 80 БАЛОВ . Решите пожалуйста . Меня неделю не было , я пропустил тему .
Приложения:

Ответы
Автор ответа:
1
Ответ:
Объяснение:
!!!!!!!!!!!!!!!!!!!!!!.!!!!!!!
Приложения:
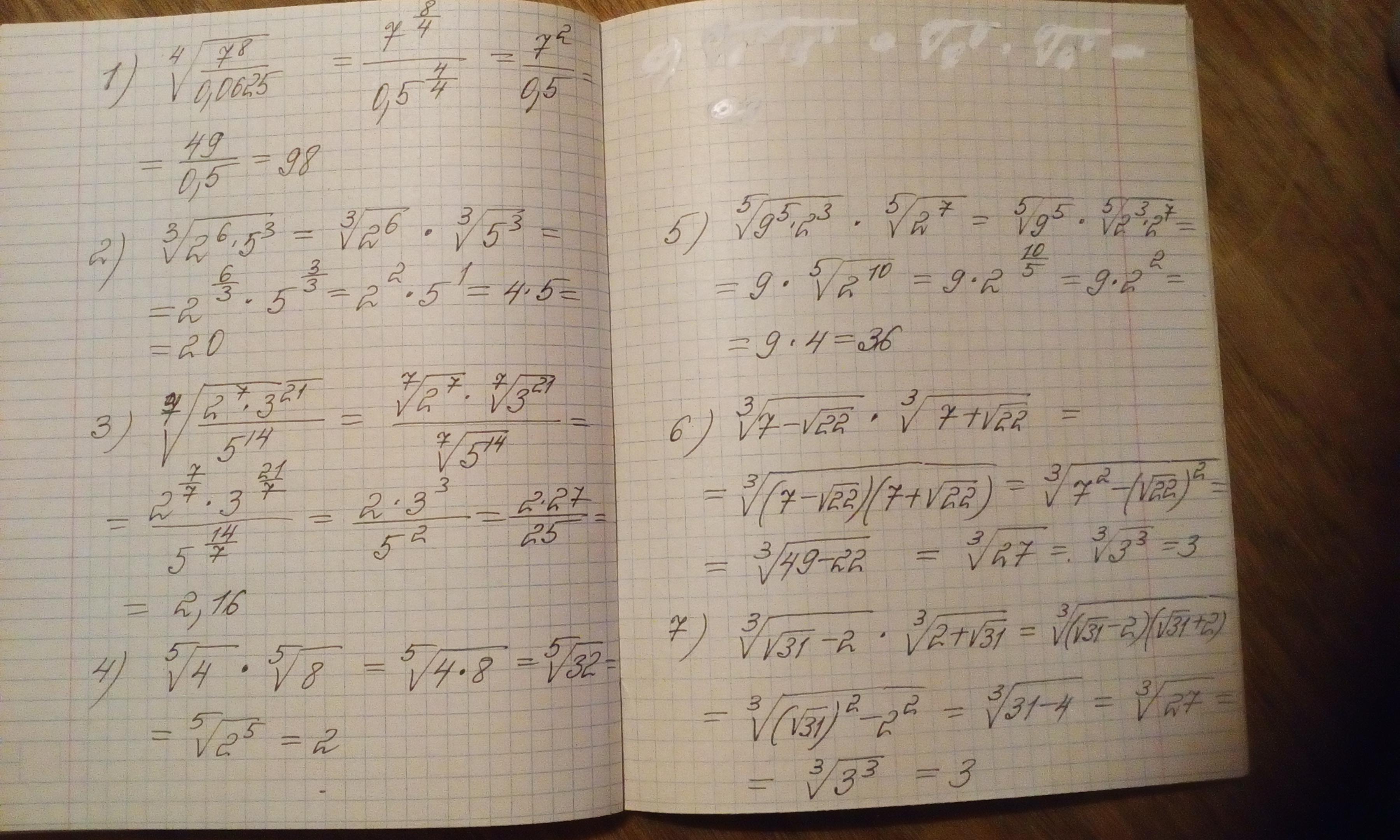
samoiluk04:
Спасибо огромное !!!
https://znanija.com/task/38732030 срочно, желательно на тетрадном листе
Автор ответа:
0
https://znanija.com/task/38732030 срочно, желательно на тетрадном листе
Похожие вопросы
Предмет: Русский язык,
автор: slrk
Предмет: Русский язык,
автор: 333Евгений333
Предмет: Русский язык,
автор: kamitina295
Предмет: Математика,
автор: EvelinkaPavlinka