Предмет: Алгебра,
автор: lanamalinovskaya51
Решить систему симметрических уравнений:
Приложения:
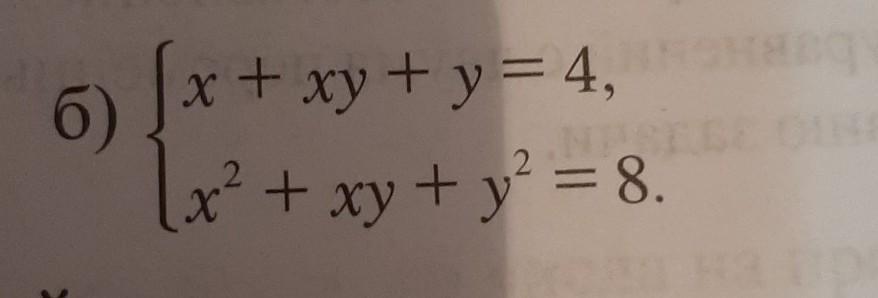
Ответы
Автор ответа:
0
Объяснение:
Пусть х+у=t, а ху=v. ⇒
Уравнение не имеет действительных корней.
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: aksel432
Предмет: Другие предметы,
автор: FlyNas
Предмет: Другие предметы,
автор: Sandro0507
Предмет: Математика,
автор: 1232348
Предмет: Алгебра,
автор: valeriyanikola1