Предмет: Геометрия,
автор: Аноним
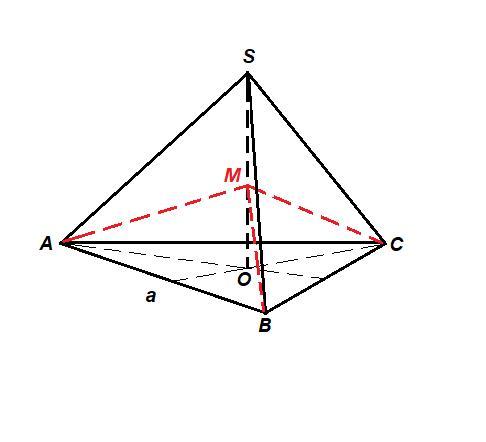
40 баллов!!!В правильном тетраэдре середина высоты соединена отрезками с вершинам основания.Докажите ,что эти отрезки взаимно перпендикулярны.
Ответы
Автор ответа:
1
Ответ:
Все ребра правильного тетраэдра равны.
Обозначим ребро а.
О - центр треугольника АВС.
По формуле радиуса окружности, описанной около правильного треугольника:
Из прямоугольного треугольника SAO по теореме Пифагора:
Из прямоугольного треугольника МАО по теореме Пифагора:
ΔMOA = ΔMOB = ΔMOC по двум катетам, ⇒
Для ΔАМВ выполняется теорема, обратная теореме Пифагора:
Значит, ΔАМВ прямоугольный.
ΔAMB = ΔAMC = ΔBMC по трем сторонам, т.е.
МА, МВ и МС взаимно перпендикулярны.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: kurbonova78
Предмет: Русский язык,
автор: yliafmenko
Предмет: Русский язык,
автор: galkin557
Предмет: Математика,
автор: apilisinka
Предмет: Математика,
автор: елизавета266