ПОМОГИТЕ ПЛИЗ
!!!!!!!!!!!!!!!!!!!!!!!!!!!
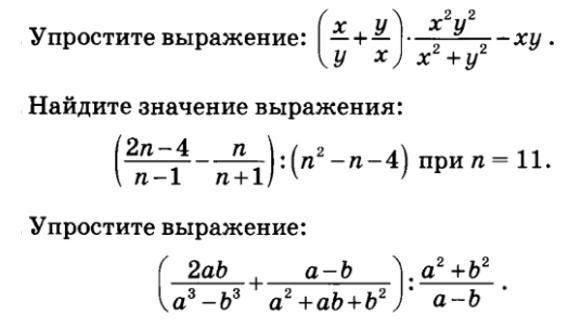
Ответы
Ответ:
В решении.
Объяснение:
1. Упростить:
(х/у + у/х) * (х²у²)/(х²+у²) - ху= 0.
1) В скобках:
х/у + у/х=
общий знаменатель ху:
=(х*х + у*у)/ху=
=(х² + у²)/ху;
2) Умножение:
[(х² + у²)/ху] * [(х²у²)/(х²+у²)]=
=[(х² + у²) * (х²у²)] / [xy * (х²+у²)]=
сократить (разделить) (х²+у²) и (х²+у²) на (х²+у²), х²у² и xy на xy:
=ху;
3)Вычитание:
ху - ху = 0.
2. Найти значение выражения:
[(2n-4)/(n-1) - n/(n+1)] : (n²-n-4)= 1/120. при n=11.
1) В скобках:
(2n-4)/(n-1) - n/(n+1)=
общий знаменатель (n-1)(n+1):
=[(n+1)*(2n-4) - (n-1)*n]=
=[(2n²-4n+2n-4) - (n²-n)] / [(n-1)(n+1)]=
=(2n²-2n-4-n²+n) / [(n-1)(n+1)]=
=(n²-n-4) / [(n-1)(n+1)];
2)Деление:
(n²-n-4) / [(n-1)(n+1)] : (n²-n-4)=
=(n²-n-4) / [(n-1)(n+1)] * (n²-n-4)=
сократить (разделить) (n²-n-4) и (n²-n-4) на (n²-n-4):
=1 / [(n-1)(n+1)]=
=1 / (n²-1)=
=1/(11²-1)=
=1/121-1)=
1/120.
3. Упростить:
[(2ab/(a³-b³) + (a-b)/(a²+ab+b²)] : [(a²+b²)/(a-b)]= 1/(a²+ab+b²).
1) В скобках:
(2ab/(a³-b³) + (a-b)/(a²+ab+b²)=
a³-b³= (a-b)(a²+ab+b²);
общий знаменатель (a-b)(a²+ab+b²):
=[(1*2ab + (a-b)*(a-b)] / (a-b)(a²+ab+b²)=
=(2ab+a²-2ab+b²) / (a-b)(a²+ab+b²)=
=(a²+b²) / (a-b)(a²+ab+b²);
2) Деление:
(a²+b²) / (a-b)(a²+ab+b²) : [(a²+b²)/(a-b)]=
=[(a²+b²) * (a-b)] / [(a-b)(a²+ab+b²) * (a²+b²)]=
сократить (a²+b²) и (a²+b²) на (a²+b²), (a-b) и (a-b) на (a-b):
=1/(a²+ab+b²).