Question

На координатной плоскости изобразим множество точек, координаты которых удовлетворяют неравенству |3х – 2y| ≤ 4 даю все баллы помогите пожалуйста прошу только нормальный ответ​

Answer 1

Ответ и Объяснение:

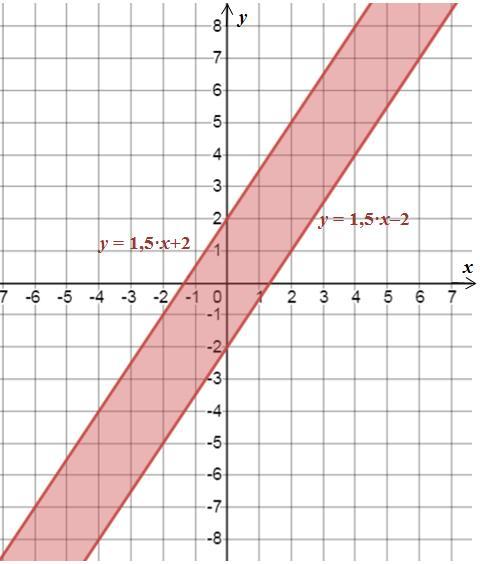
Граница множества |3·x – 2·y| ≤ 4 определяется по формуле:

|3•х – 2•y| = 4.

По определению модуля получаем:

3•х – 2•y = –4 ⇔ 2•y = 3•х + 4  ⇔ y = 1,5•х + 2  

3•х – 2•y = 4 ⇔ 2•y = 3•х – 4  ⇔ y = 1,5•х – 2  

Каждое из этих функций линейное, поэтому для построения достаточно определить по 2 точек:

y = 1,5•х + 2 :

1) y(0)= 1,5•0 + 2 = 2 → (0; 2); 2) y(2)= 1,5•2 + 2 = 5 → (2; 5);

y = 1,5•х – 2 :

1) y(0)= 1,5•0 – 2 = –2 → (0; –2); 2) y(–2)= 1,5•(–2) + 2 = –1 → (–2; –1).

Рисунок в приложении.