Предмет: Алгебра,
автор: aruka3064
помогите 2.1, 2.2,2.3
Приложения:
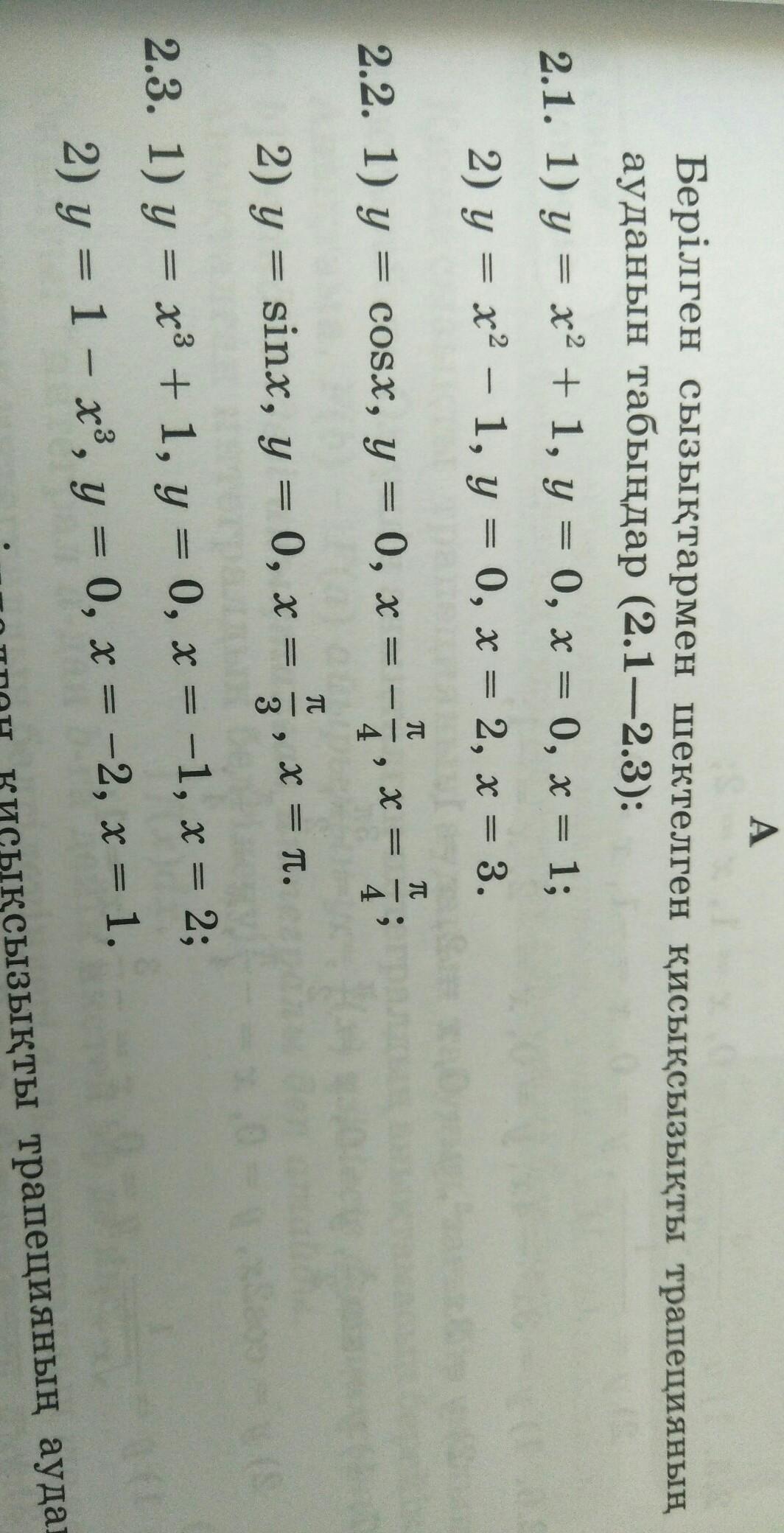
sangers1959:
Найти площадь с помощью интеграла?
Найдите площадь криволинейной трапеции, ограниченную заданными линиями
да
Ответы
Автор ответа:
1
Ответ:
Объяснение:
2.1.
Ответ: S≈1,3333 кв. ед.
Ответ: S≈5,3333 кв.ед.
2.2.
Ответ: S≈1,4142 кв.ед.
Ответ: S=1,5 кв.ед.
2.3.
Ответ: S=6,75 кв. ед.
Ответ: S=6,75 кв. ед.
Похожие вопросы
Предмет: Українська мова,
автор: kraVetssss
Предмет: Русский язык,
автор: derwisheva18
Предмет: Русский язык,
автор: krasnosheckova
Предмет: История,
автор: volk9078
Предмет: Алгебра,
автор: лардис