Предмет: Алгебра,
автор: lizapanzova2005
Докажите неравенствa
1) a²+b² ≥ 2(a+b-1)
2) 2a²+b²+c² ≥ 2a(b+c)
lizapanzova2005:
Спасибо вам огромное вы мне очень помогли)))
ну мы же команда)
Если вам не сложно, можете помочь с ещё двумя неравенствами?)))
мне не сложно. у меня горит с ца блица
сейчас я пробомблю, посмотрю
Спасибочки)
Ну так, что поможешь?
Ответы
Автор ответа:
4
Ответ:
На фото
Объяснение:
Квадрат выражения всегда (кроме комплексных чисел) ≥ 0
Приложения:
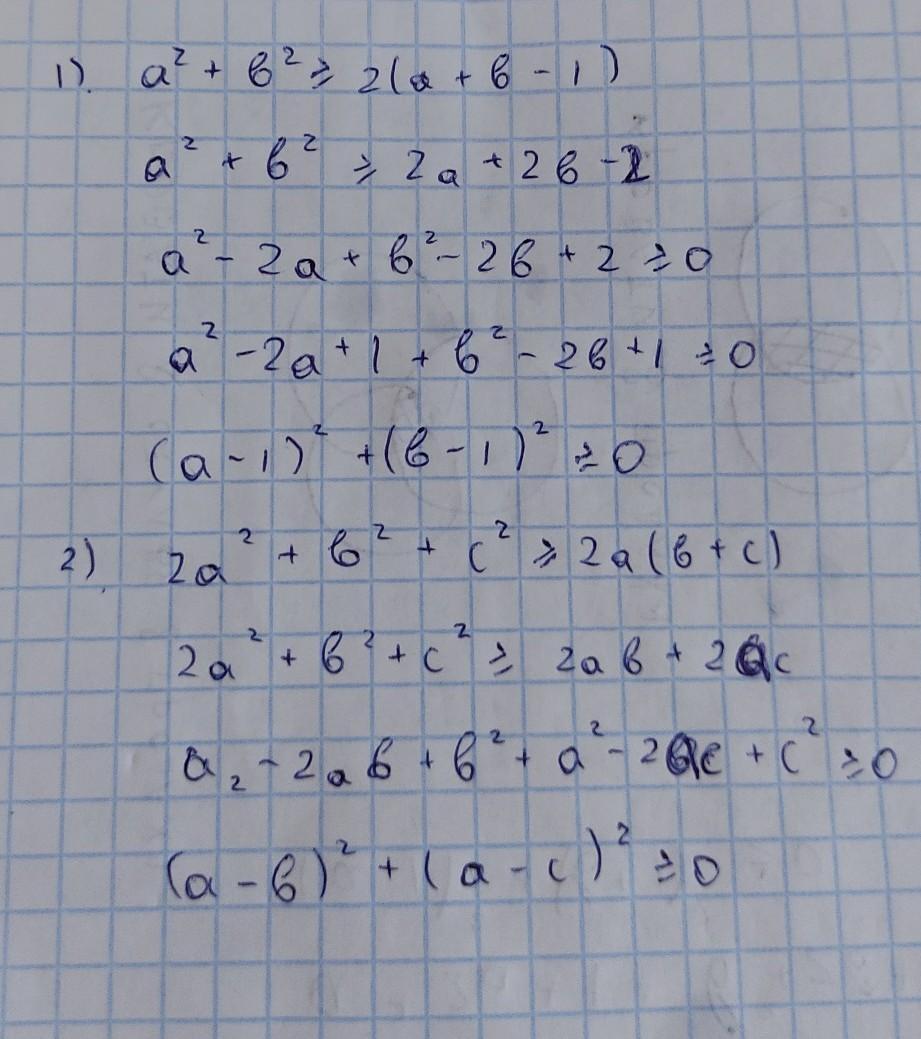
Спасибо
Всегда пожалуйста
а почему a^2+2a+1? вроде минус должен быть, мы же с обратным знаком переносим
Да
Сейчас исправлю
пожалуйста помогите с программированием.Даю много баллов
Автор ответа:
2
1)
Раскрываем скобки
Переносим все в левую часть
Рассмотрим слагаемые отдельно друг от друга
Если слагаемые больше или равны 0, то их сума будет больше или равна 0
ЧТД
2)
Раскроем скобки
Переносим все в левую часть
Далее рассмотрим отдельно слагаемые
Раз слагаемые больше или равны 0, то и их сумма будет больше, либо равна 0
ЧТД
Спасибо
не за что
Похожие вопросы
Предмет: Русский язык,
автор: constantinovi42
Предмет: Русский язык,
автор: olga1980r
Предмет: Другие предметы,
автор: elite79
Предмет: Химия,
автор: maraharta
Предмет: Математика,
автор: nadyushagerasi1