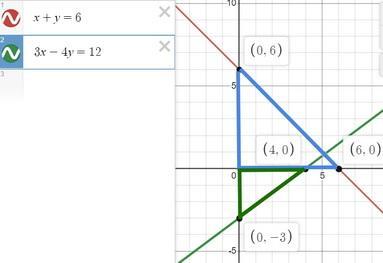
Найдите площадь треугольника, ограниченного осями координат и прямой a) x + y = 6 b) 3x-4y = 12
Ответы
Ответ:
Объяснение:
определимся с размерами наших треугольников
а) х + у = 6
катетами треугольника являются оси ох и оу от точки (0;0) до точки пересечения графика с осями точки (х₀; у₀) и (х₁; у₁)
- точка пересечения графика с осью оу (при х₀ = 0 у₀ = 6) точка (0; 6)
расстояние от (0;0) до точки (0;6) по оси оу - это модуль координаты у₀ у₀= |6| = 6 - это длина одного катета
- аналогично точка пересечения с осью ох (при у₁=0 х₁ = 6) точка (6;0)
расстояние от (0;0) до точки (0;6) по оси ох - это модуль координаты х₁ |х₁| = |6 | = 6 - это длина другого катета
ну, и площадь - это полупроизведение катетов S = x₁*y₀/2 =6*6/2 =18
ответ S = 18
b) 3x-4y = 12
все аналогично
точки пересечения графика с осями:
- оу (0; -3), расстояние от этой точки до точки (0;0) это |y₀| = |-3| =3
это длина одного катета 3
- с осью ох (при у₁=0 х₁ = 6) точка (6;0)
расстояние от (0;0) до точки (0;4) по оси ох - это модуль |x₁| = |4|=4
это длина другого катета 4
площадь - S = x₁*y₀/2 =3*4/2 =6
ответ S = 6