Предмет: Геометрия,
автор: vanilla7549
в треугольнике abc am-медиана ,ab =a ,ac=b , выразите векторы MA ,BC , MB через векторы a и b
Ответы
Автор ответа:
3
Ответ:
Объяснение:
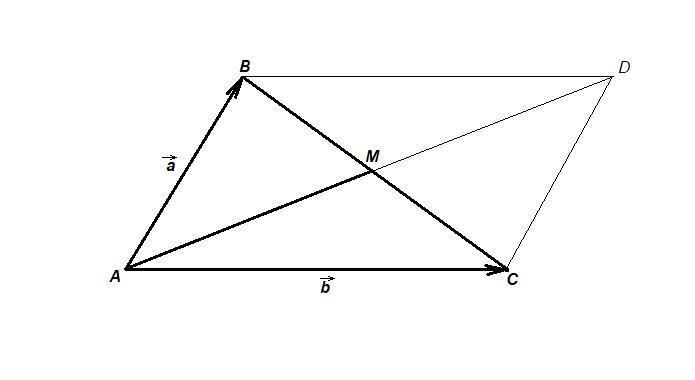
Достроим треугольник до параллелограмма.
Диагонали параллелограмма точкой пересечения делятся пополам.
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Русский язык,
автор: Lllllllllll222
Предмет: Русский язык,
автор: REMBER
Предмет: Математика,
автор: Аноним