Предмет: Алгебра,
автор: mifort902
Помогите срочно, кто чем можнт1
Приложения:
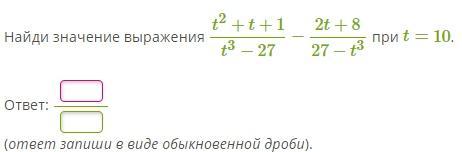
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Поскольку t=10, то
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: гюнель01
Предмет: Українська мова,
автор: Daniel19992014
Предмет: Русский язык,
автор: frants96
Предмет: Литература,
автор: Аноним