Предмет: Алгебра,
автор: lilo1111110
помогите решить уравнение
Приложения:
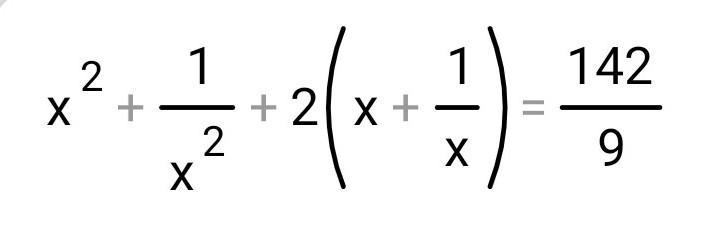
Ответы
Автор ответа:
1
Замена:
Можно решить через дискриминант, но в данном случае также удобно выделить полный квадрат:
Обратная замена:
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: nimhain
Предмет: Русский язык,
автор: Nastya12Vezhlivceva
Предмет: Русский язык,
автор: bbk203
Предмет: Биология,
автор: Аноним
Предмет: Математика,
автор: Puskus8888