4. Высота правильной треугольной пирамиды равна 3/3 см, а угол
между апофемой и плоскостью основания пирамиды — 60°. Вы-
числите площадь полной поверхности пирамиды.
Ответы
Ответ:
3√3 см²; 81√3 см².
Объяснение:
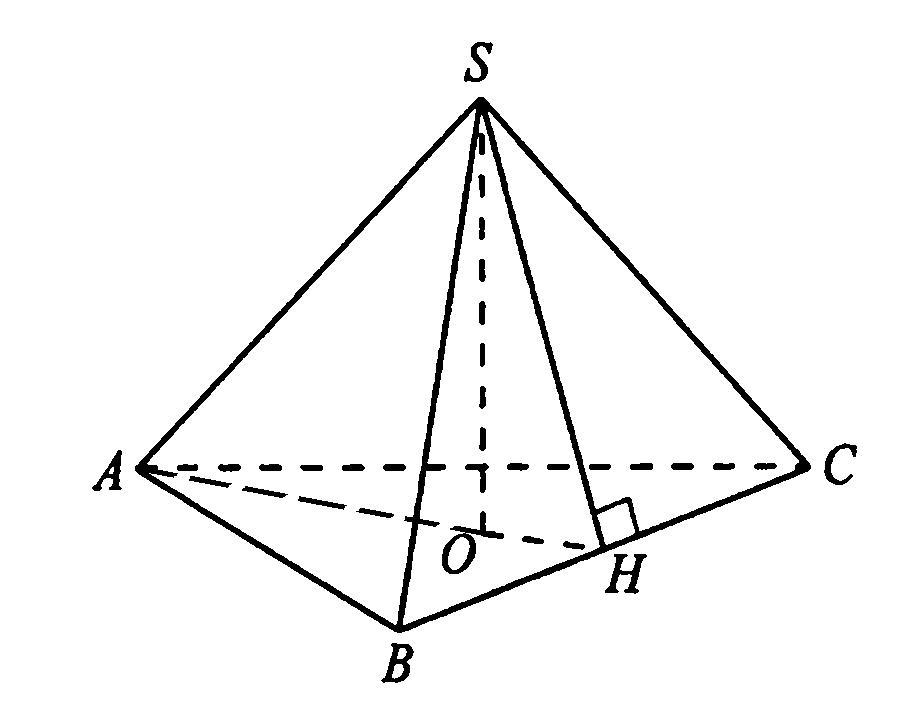
Обозначим данную пирамиду буквами SABC.
SO = h см (высота пирамиды).
SH - апофема.
∠SHO = 60°.
========================================================
ΔSHO - прямоугольный.
Если угол прямоугольного треугольника равен 60°, то напротив лежащий катет равен произведению меньшего катета на √3.
⇒ SO = OH * √3 = h см ⇒ OH = SO : √3 = h : √3 = √3h/3 см.
По свойству прямоугольного треугольника, ∠OSH = 90° - ∠SHO = 90° - 60° = 30°.
Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.
⇒ SH = OH * 2 = √3h/3 * 2 = 2√3h/3 см.
По свойству правильной треугольной пирамиды, ΔABC - правильный.
Точка O - точка пересечения медиан, которая делит их в отношении 2:1, считая от вершины.
OH = 1/3 * AH, AO = 2/3 * AH ⇒ AH = OH + AO = OH * 3 = √3h/3 * 3 = √3h см.
По свойству правильного треугольника, AH - высота.
AH = AB√3/2 = √3 см ⇒ AB = AH * 2/√3 = √3h * 2/√3 = 2h см.
Значит AB = BС = AC = 2h см.
⇒ P ΔABC = AB + BC + AC = AB * 3 = 2h * 3 = 6h см.
S бок. поверхн. = 1/2 * P ΔABC * SH = 1/2 * 6h * 2√3h/3 = 2√3h² см²
S осн. = 1/2 * AH * BC = 1/2 * √3h * 2h = √3h² см²
S полн. поверхн. = S бок. поверхн. + S осн. = 2√3h² + √3h² = 3√3h² см²
Рассмотрим два случая значения h: h = 3√3 см и h = 3/3 см.
Подставим эти значения в решение и вычислим площадь полной поверхности. В итоге:
При значении h = 3√3 см S полн. поверхн. = 81√3 см².
При значении h = 3/3 см = 1 см S полн. поверхн. = 3√3 см².