Question

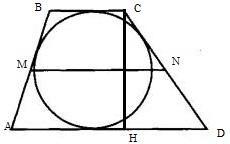
Вокруг окружности описали равнобокую трапецию. Найдите высоту этой трапеции, если один из углов ее равен 150°, средняя линия 24 см.​

Answer 1

Пусть ABCD — равнобокая трапеция, MN — средняя линия трапеции, MN = 24 см, ∠ABC = ∠BCD = 150°, то ∠CDA = ∠BAD = 30°.

У четырехугольника, описанного вокруг окружности, сумма противоположных сторон равны. Следовательно, сумма оснований трапеции, равна AD + BC = 2MN = 48 см.

AB + CD = AD + BC

2CD = 48

CD = 24 см

Против угла 30° катет в два раза меньше гипотенузы, то есть, высота трапеции CH=24:2 = 12 см