Question

Квадратный трехчлен ax2+bx+c с ненулевыми коэффициентами имеет два рациональных корня. Может ли один или два его коэффициента быть иррациональными? 50 баллов!!!!!!!!!!!!!!!

Answer 1

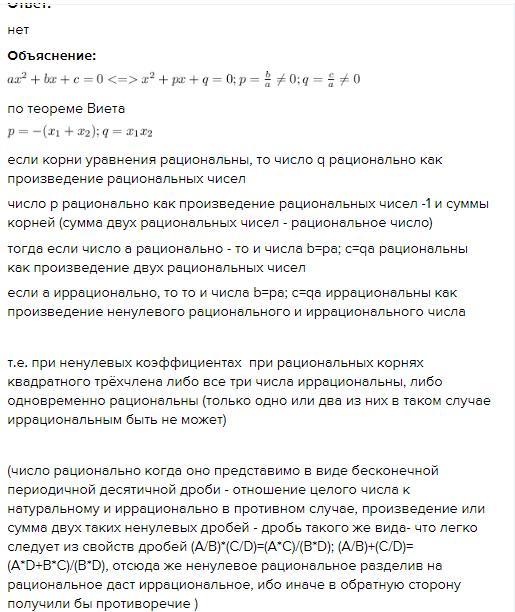
Ответ:

нет

Объяснение:

$ax^2+bx+c=0 <=> x^2+px+q=0; p=\frac{b}{a} \neq 0; q=\frac{c}{a} \neq 0$

по теореме Виета

$p=-(x_1+x_2); q=x_1x_2$

если корни уравнения рациональны, то число q рационально как произведение рациональных чисел

число р рационально как произведение рациональных чисел -1 и суммы корней (сумма двух рациональных чисел - рациональное число)

тогда если число а рационально - то и числа b=pa; c=qa рациональны как произведение двух рациональных чисел

если а иррационально, то то и числа b=pa; c=qa иррациональны как произведение ненулевого рационального и иррационального числа

т.е. при ненулевых коэффициентах  при рациональных корнях квадратного трёхчлена либо все три числа иррациональны, либо одновременно рациональны (только одно или два из них в таком случае иррациональным быть не может)

(число рационально когда оно представимо в виде бесконечной периодичной десятичной дроби - отношение целого числа к натуральному и иррационально в противном случае, произведение или сумма двух таких ненулевых дробей - дробь такого же вида- что легко следует из свойств дробей (A/B)*(C/D)=(A*C)/(B*D); (A/B)+(C/D)=(A*D+B*C)/(B*D), отсюда же ненулевое рациональное разделив на рациональное даст иррациональное, ибо иначе в обратную сторону получили бы противоречие )