Question

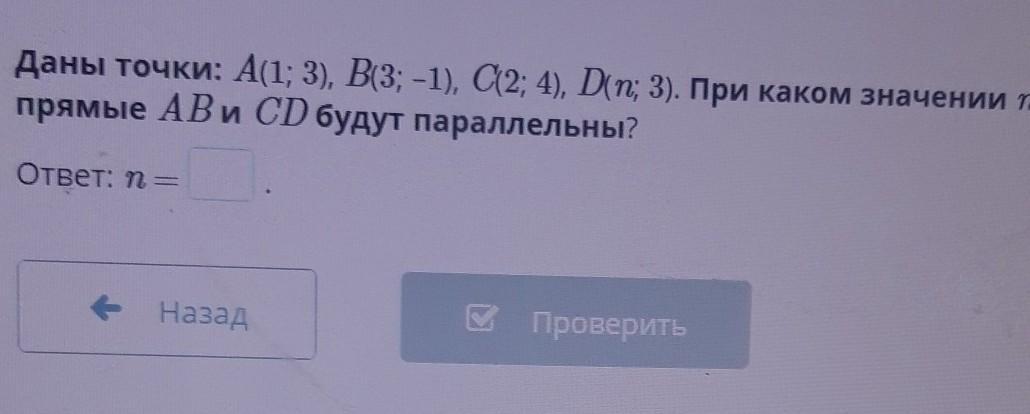
Даны точки: A(1; 3), B(3; –1), C(2; 4), D(n; 3). При каком значении n прямые AB и CD будут перпендикулярны?​

Answer 1

Ответ:

Объяснение:

Имеем две прямые:

y=k₁x+b₁   и    y=k₂x+b₂

Они будут параллельны, если k₁=k₂ и b₁≠b₂.

1) Найдем уравнение первой прямой AB, проходящей через точки А(1;3) и В(3;-1). Составим систему уравнений и решим методом сложения:

$\displaystyle \left \{ {{3=k_1*1+b_1} \;\;\;|*(-1)\atop {-1=k_1*3+b_1}} \right. \\\\+\left \{ {{-3=-k_1-b_1} \atop {-1=3k_1+b_1}} \right. \\-4=2k_1\\k_1=-2\\-1=3*(-2)+b_1\\-1=-6+b_1\\b_1=5$

Получили уравнение первой прямой:

$\displaystyle y=-2x+5$

2) Найдем уравнение второй прямой AD, проходящей через точки С(2;4) и D(n;3):

$\displaystyle \left \{ {{4=k_2*2+b_2} \;\;\;|*(-1)\atop {3=k_2*n+b_2}} \right. \\\\+\left \{ {{-4=-2k_2-b_2} \atop {3=k_2n+b_2}} \right. \\\\-1=-2k_2+k_2n\\k_2(n-2)=-1\\\\k_2=\frac{1}{2-n}$

Условие параллельности: k₁=k₂

$\displaystyle -2=\frac{1}{2-n}\;\;\;|*(2-n);\;n\neq 2 \\-2(2-n)=1\\-4+2n=1\\2n=5\\n=2,5$

Проверим, равны ли b₁ и b₂.

Подставим k₂=-2 в первое уравнение системы:

$\displaystyle 4=2*(-2)+b_2\\4=-4+b_2\\b_2=8$

Тогда второе уравнение имеет вид:

$y=-2x+8$

k₁=k₂=-2 при n=2,5. При этом b₁≠b₂.

Условие параллельности соблюдено.