Предмет: Алгебра,
автор: Shawol2
Найдите предел с объяснением, пожалуйста
Приложения:
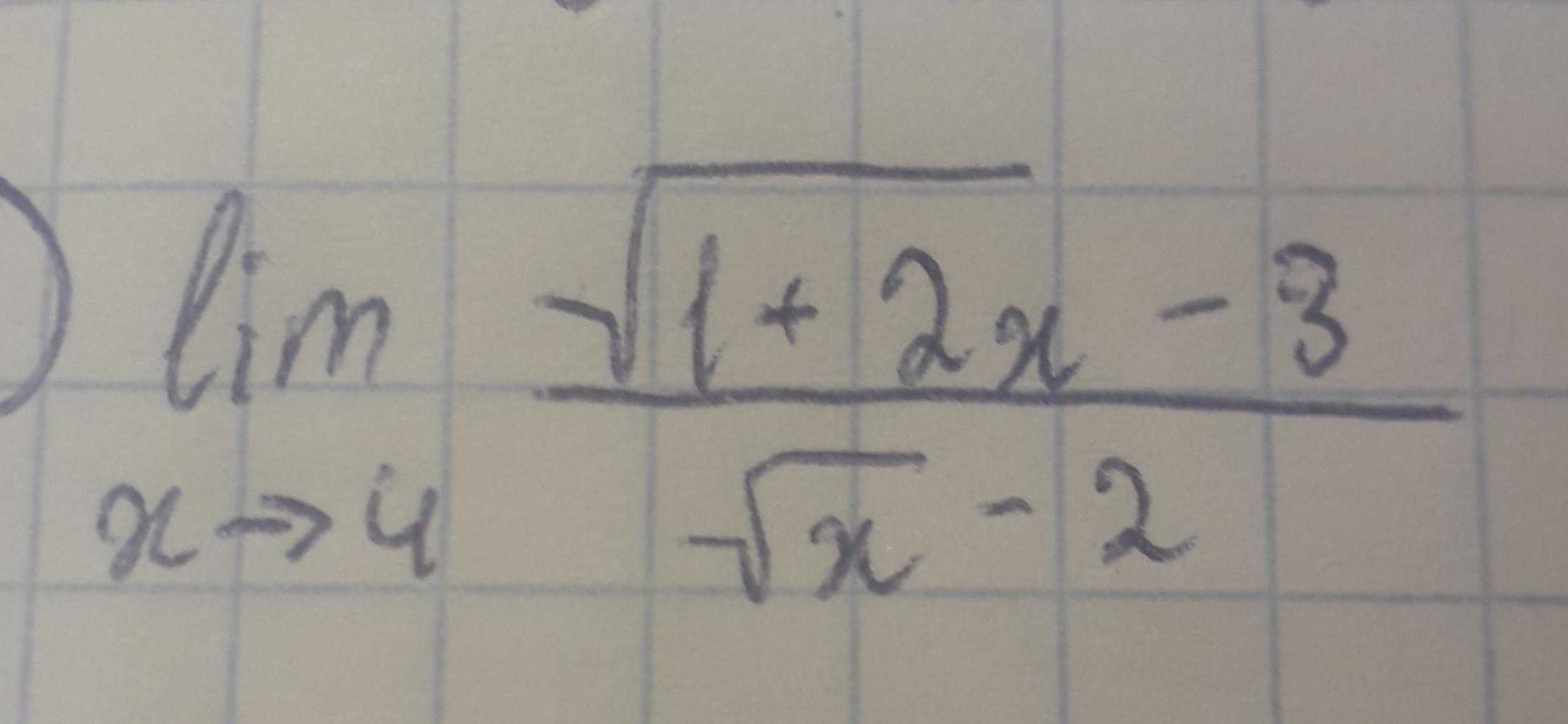
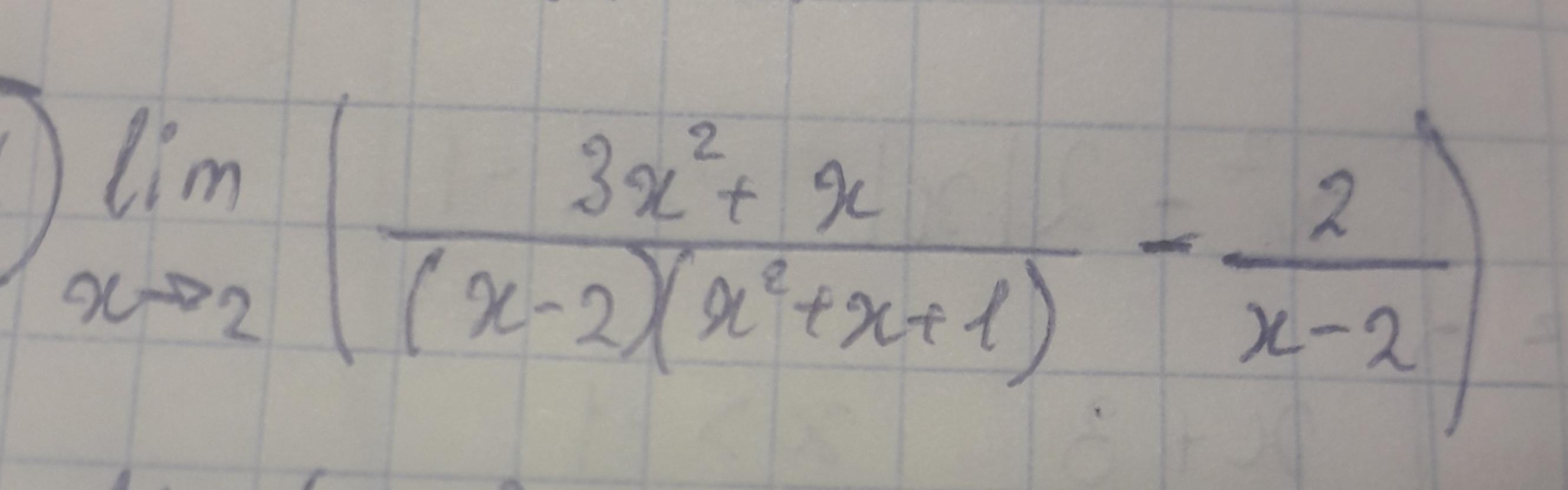
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Українська мова,
автор: alinka16112003
Предмет: Русский язык,
автор: malinka250
Предмет: Другие предметы,
автор: пацанце
Предмет: Математика,
автор: Ярик55555
Предмет: Литература,
автор: друг90