Question

помогите пожалуйста с геометрией.очень надо срочно. с рисунком и полным решением. сторона основания правильной четырехугольной пирамиды равна 10, боковые грани наклонены к основанию под углом 60.в эту пирамиду вписан цилиндр,одно основание которого о лежит в плоскости основания пирамиды,а окружность верхнего основания касается боковой поверхности пирамиды.найдите площадь боковой поверхности цилиндра если радиус основание 2

Answer 1

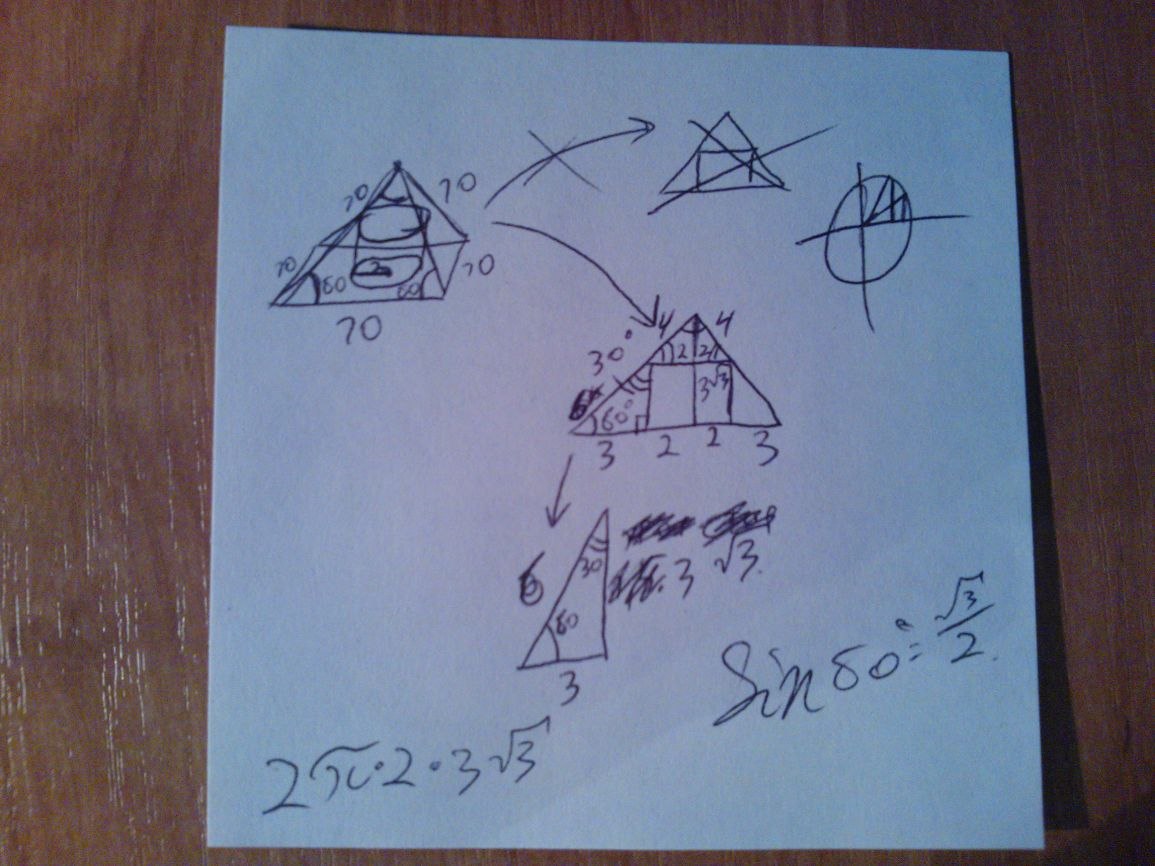
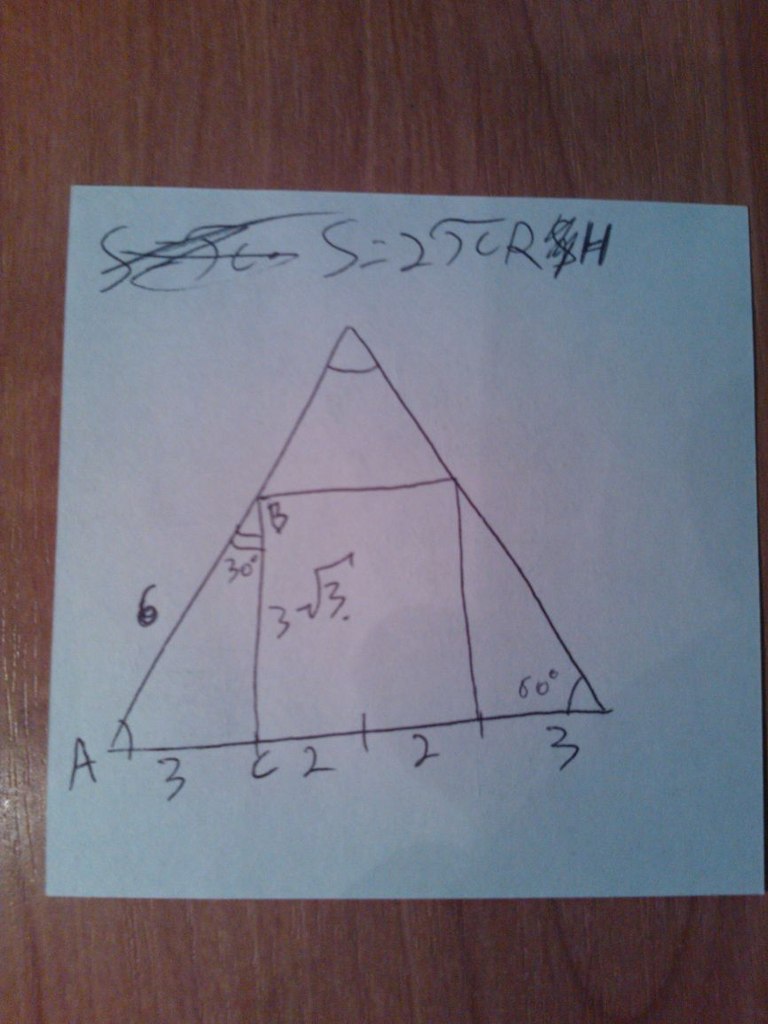
Берем  вертикальное сечение по центру пирамиды (или проекцию). Т.к. углы наклона боковых грней равны 60 гр., то и третий угол будет равен 60. В проекции берём треугольник АВС, где АС = 3. Т.к. сторона АС находится напротив угла в 30 градусов, то гипотенуза АВ = 6. Sin 60 = Sqrt(3)/2, а значит ВС относится к АВ как корень из трёх к двум, => ВС=Sqrt(3)*3. По формуле S=2ПRH получаем, что S=2*3.14*2*3*Sqrt(3)=37.68*Sqrt(3)=~65.26