Question

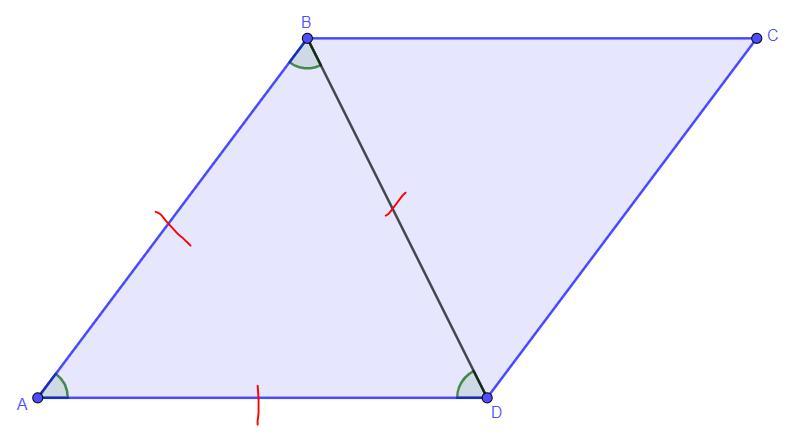
4.Один из углов ромба равен 120

°, а диагональ, исходящая из вершины этого угла равна 12см. Найдите периметр ромба​

Answer 1

Ответ:

$\boxed{P_{ABCD} = 48}$ см

Объяснение:

Дано: ABCD - ромб, ∠ABC = 120°, BD = 12 см

Найти: $P_{ABCD}$ - ?

Решение: По свойствам ромба его противоположные стороны параллельны, тогда AD║BC. Так как AD║BC, то угол ∠BAD + ∠ABC = 180° как соответственные углы при параллельных прямых, тогда

∠BAD = 180°- ∠ABC = 180° - 120° = 60°. Так как по свойствам ромба его противоположные углы равны и диагональ является биссектрисой для углов ромба, то угол ∠ABD = ∠CBD = ∠ADB = ∠CDB = 120° : 2 = 60°. Так как в треугольнике ΔBAD все углы равны 60°( ∠BAD = ∠ABD = ∠ADB = 60°), то по теореме треугольник ΔBAD - правильный, тогда все его стороны равны и AB = BD = AD = 12 см. Так как по свойствам ромба все его стороны равны, то AD = BC = AB = CD = 12 см. Так как периметр ромба это сумма всех его сторон, то $P_{ABCD} = AD + BC + AB + CD = 12 + 12 + 12 + 12 = 48$ см.