Предмет: Алгебра,
автор: mrr34
Помогите пожалуйста с 5 заданием, найти производную функцию
Приложения:
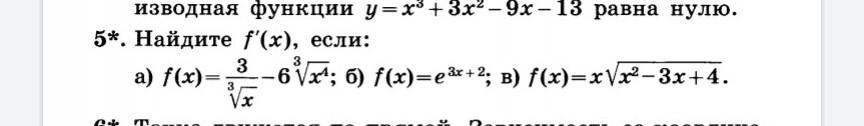
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: GoLdErMeN
Предмет: Українська мова,
автор: dybskyi123
Предмет: Другие предметы,
автор: schernikow
Предмет: Математика,
автор: angelinavahodova
Предмет: Математика,
автор: Dioxide1