Предмет: Геометрия,
автор: velis50
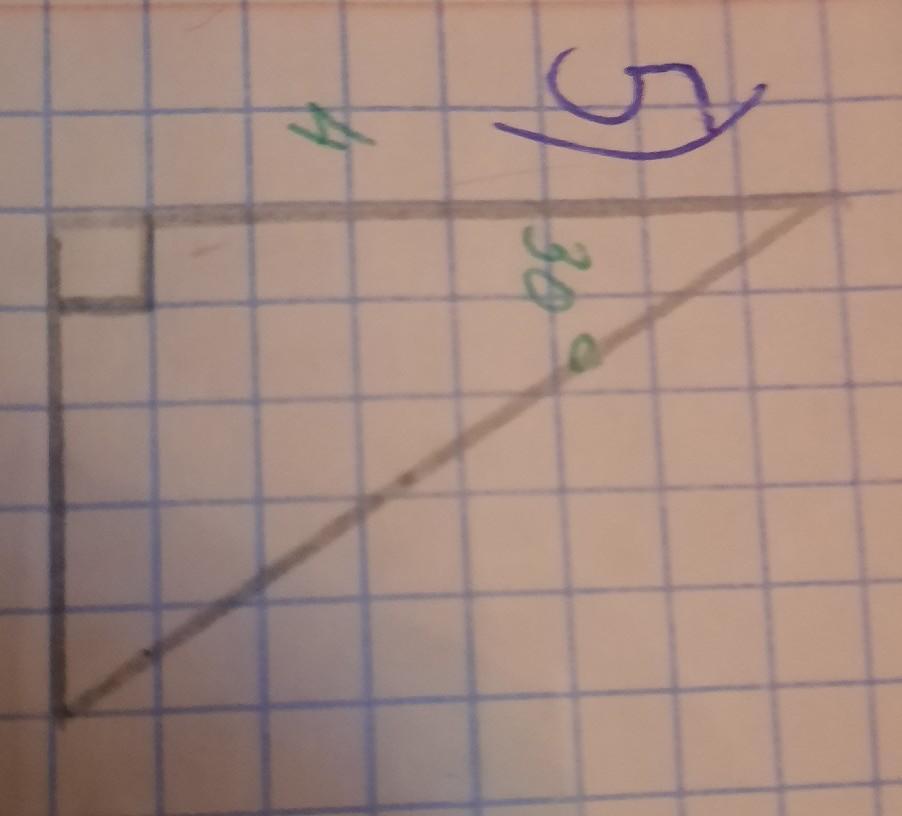
катет равен 4, а прилежащий к нему угол 30 градусам. Найти гипотенузу и второй катет.
Приложения:
Ответы
Автор ответа:
0
Ответ
ед. - гипотенуза,
ед. - катет
Объяснение:
Рассмотрим прямоугольный треугольник АВС.
∠А= 30°, катет АС=4 ед.
По свойству катета, лежащего напротив угла в 30°: в прямоугольном треугольнике катет лежащий напротив угла в 30° равен половине гипотенузы.
Тогда
Пусть ВС= х ед.. Тогда АВ=2х ед. По теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
так как х - катет и выражен положительным числом.
Тогда катет ед.,
а гипотенуза ед.
Приложения:

Похожие вопросы
Предмет: Английский язык,
автор: irinaisa25
Предмет: Русский язык,
автор: snezhanazaya
Предмет: Русский язык,
автор: maloli
Предмет: Математика,
автор: nastyaSeleznev
Предмет: Алгебра,
автор: omarbek170623