Предмет: Алгебра,
автор: batirgereevasau1
Решите этот интеграл
Приложения:
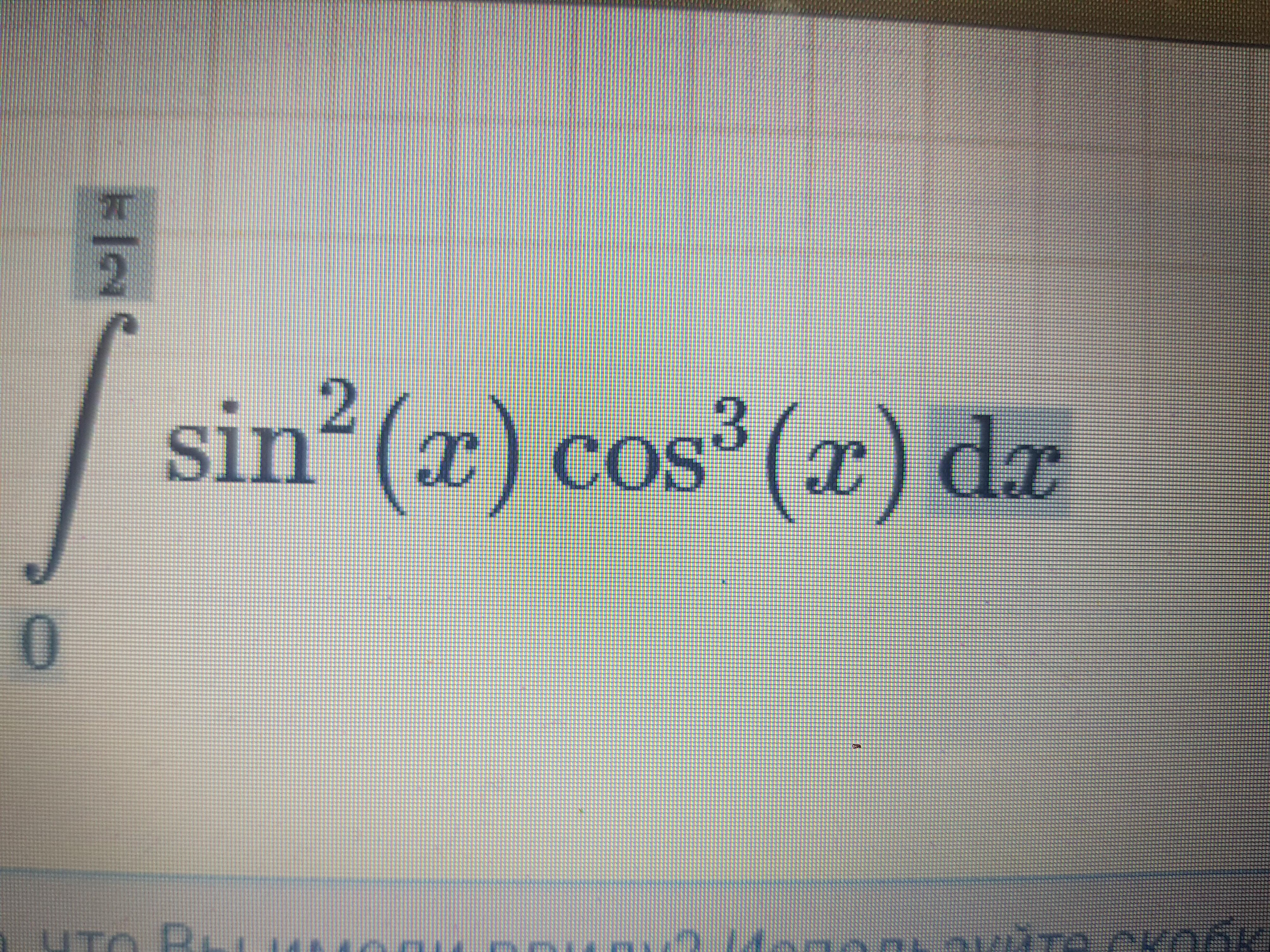
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Теперь интеграл запишется, как
Делаем замену переменной y=sin(x), получаем
Похожие вопросы
Предмет: Українська література,
автор: antoshka8011
Предмет: Другие предметы,
автор: АнстасияКотова
Предмет: Русский язык,
автор: maxim55546
Предмет: Химия,
автор: viktoriyagarga
Предмет: Алгебра,
автор: AliceKey