Предмет: Алгебра,
автор: ВладимирБ
Решить уравнение
——————————-
Приложения:
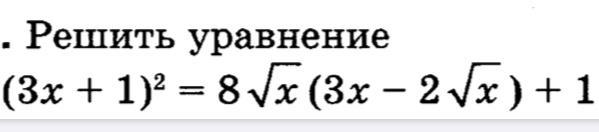
Ответы
Автор ответа:
2
если надо действительные, то одз x ≥ 0
(3x + 1)² = 8√x(3x - 2√x) + 1
9x² + 6x + 1 = 24x√x - 16x + 1
9x² + 22x - 24x√x = 0
x(9x + 22 - 24√x) = 0
x = 0 если x ∈ R то это одно
9x - 24√x + 22 = 0
√x = t
9t² - 24t + 22 = 0
D = 24² - 4*9*22 = -216
t12 = (24 +- 6i√6)/18 = (4 +- i√6)/3
x12 = ((4 +- i√6)/3)² = (16 +- 8i√6 - 6)/9 = (10 +- 8i√6)/9 = 10/9 +- 8i√6/9
ответ 10/9 +- 8i√6/9, 0
Владимир не мог бы помочь мне с моим последним вопросом на профиле
Автор ответа:
1
Ответ:
Вводим замену:
пусть
Тогда скобку можно записать:
D/4=12^2-22×9=-54<0
Нет корней.
==>
уравнение имеет единственный
действительный корень.
Ответ: х=0; х€{R}.
Владимир не мог бы помочь мне с моим последним вопросом на профиле
Похожие вопросы
Предмет: Русский язык,
автор: VIPАлеська
Предмет: Русский язык,
автор: pavelbuynyy02
Предмет: Русский язык,
автор: irinajyravleva
Предмет: Математика,
автор: Savka562
Предмет: Математика,
автор: YULIYAIVANCOVA
это для всех или какому то классу ???