Предмет: Алгебра,
автор: ВладимирБ
Решить уравнение
......................................
Приложения:
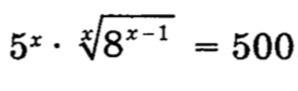
Ответы
Автор ответа:
3
Ответ:
aliyakoken:
Владимир не мог бы помочь мне с моим последним вопросом на профиле
Похожие вопросы
Предмет: Русский язык,
автор: alesya20032579
Предмет: Русский язык,
автор: Nikolettta
Предмет: Русский язык,
автор: АлинаСмольянинова2
Предмет: Химия,
автор: сливка3
Предмет: Алгебра,
автор: ivanovaanastasi1