Предмет: Алгебра,
автор: Morfie
Решите уравнение(напишите полное решение, пожалуйста)
Приложения:
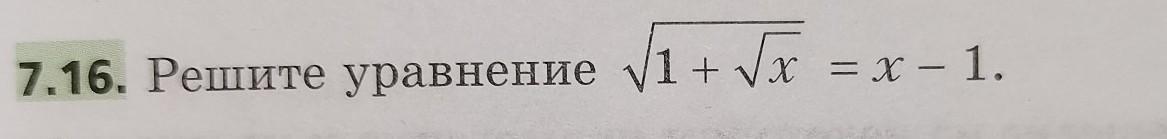
Ответы
Автор ответа:
1
Ответ:
Объяснение:
х не дорівнює 1;
з не дорівнює 0.
відповідь зверху.
dasakucenko454:
ой, там в стрічці : "х" не дорівнює 1; та "х" не дорівнює 0" то не "з" , то "х"
Похожие вопросы
Предмет: Русский язык,
автор: alexfranccat
Предмет: Английский язык,
автор: berzalinka1
Предмет: Английский язык,
автор: Milana2209
Предмет: Алгебра,
автор: zabava22
Предмет: Биология,
автор: dashagracheva2